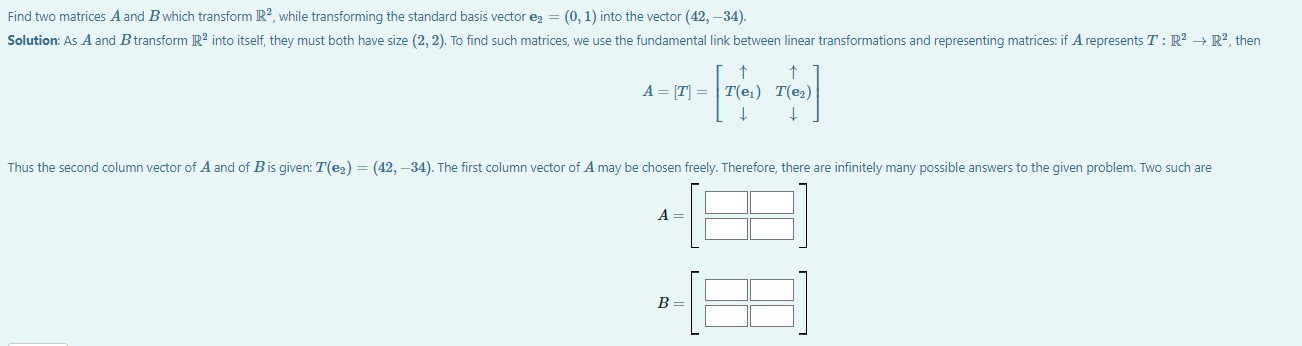
Find two matrices A and B which transform IR, while transforming the standard basis vector en = (0, 1) into the vector (42, -34). Solution: As A and B transform IR2 into itself, they must both have size (2, 2). To find such matrices, we use the fundamental link between linear transformations and representing matrices: if A represents T : IR? -> IR?, then A = [T] = T(e1) T(ez) Thus the second column vector of A and of B is given: T(e2) = (42, -34). The first column vector of A may be chosen freely. Therefore, there are infinitely many possible answers to the given problem. Two such are A = B =