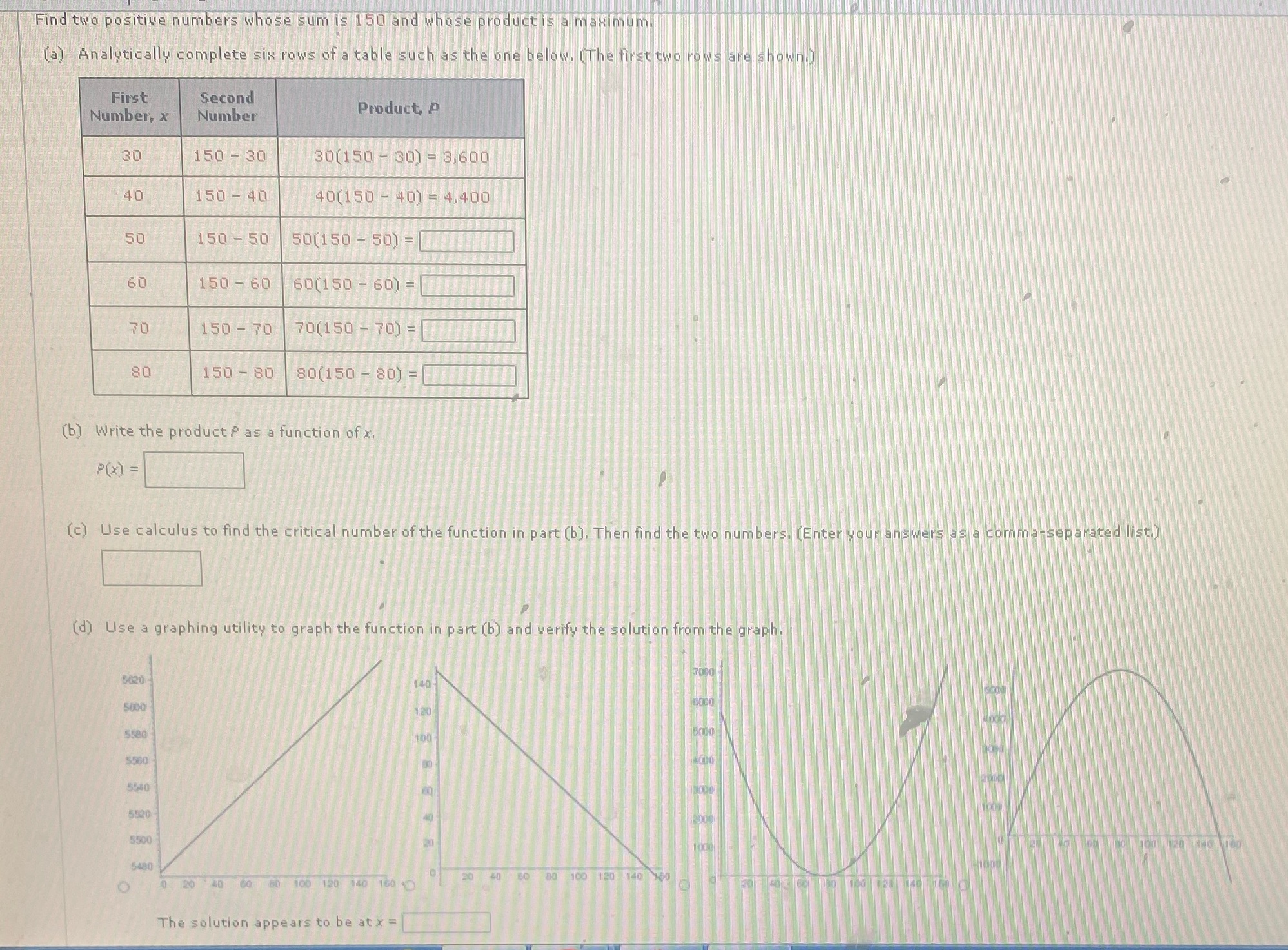
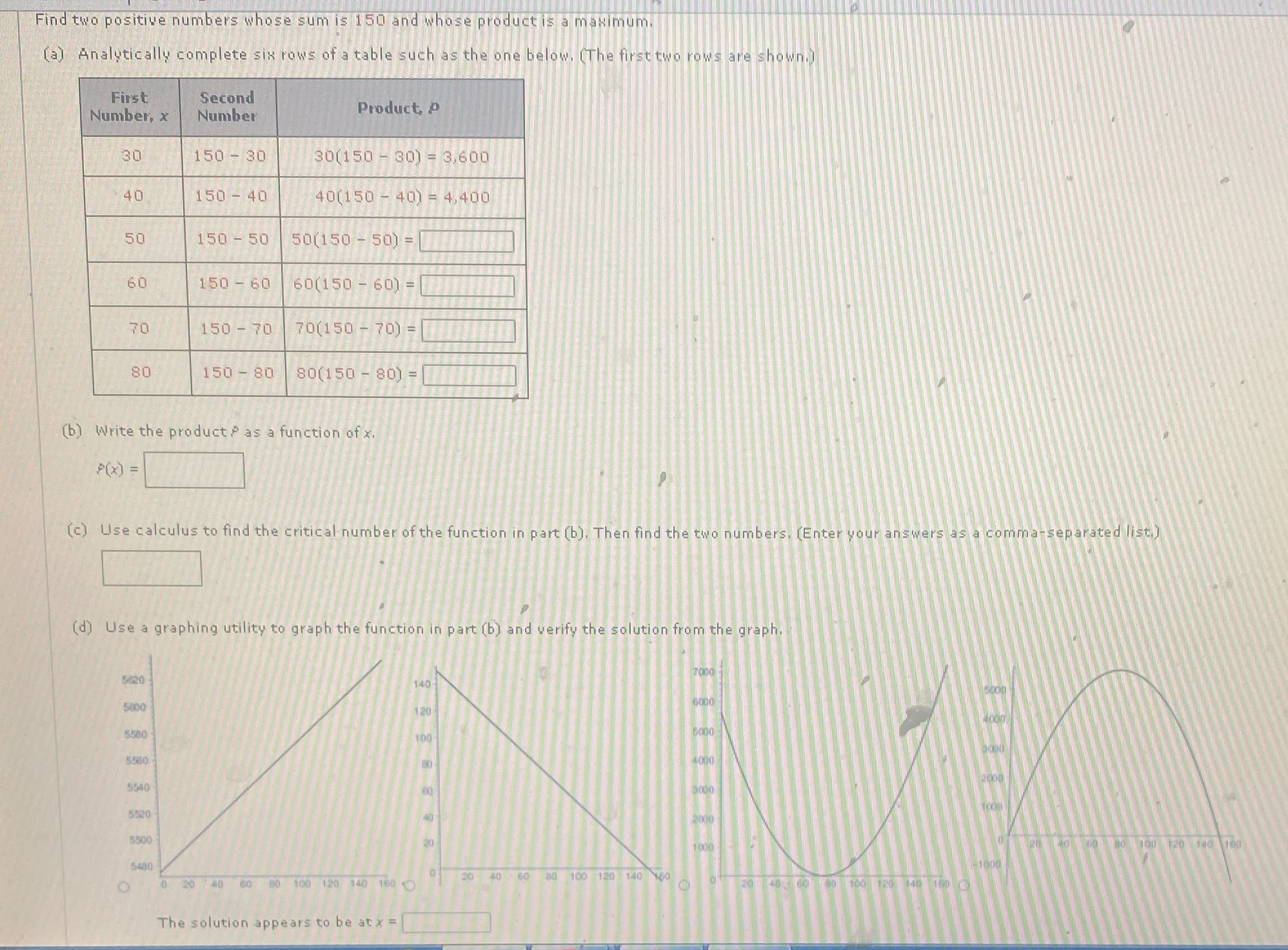
Find two positive numbers whose sum is 150 and whose product is a maximum. (al Analytically complete six rows of a table such as the one below. (The first two rows are shown First Second Number, x Number Product, p 30 150 - 30 30(150 - 30) = 3,600 40 150 - 40 40(150 - 40) = 4,400 50 150 - 50 50(150 - 50) = 60 150 - 60 60(150 - 60) = 150 - 70 70(150 - 70) = 80 150 - 80 80(150 - 80) = (b) Write the product as a function of x. P(X) = (c) Use calculus to find the critical number of the function in part (b). Then find the two numbers. (Enter your answers as a comma separated list. (d) Use a graphing utility to graph the function in part (b) and verify the solution from the graph 5620 140 5000 120 5580 160 5560 5560 5520 40 5500 1:060 5480 20 40 60 80 100 120 140 O 20 60 60 100 120 340 160 The solution appears to be at x =