Finding a Unit Tangent Vector to a Curve

Recall that a unit tangent vector to a curve in space is a vector tangent to the curve at a given point with a length of one. Recall the steps for finding a unit tangent vector and note the similarities with doing it in MATLAB:

1. Differentiate the function r=[f(t) g(t) h(t)] (where f, g, and h are anonymous functions)
2. Substitute the given value of t into the derivative to find a tangent vector (using the subs command)
3. Multiply the resulting vector by 1/magnitude to get a unit vector (using the norm command). NOTE that -1*your answer is ALSO a unit tangent vector (just in the opposite direction).

Using the steps above, find a unit tangent vector to the curve r = [cos^3( t ), sin^3( t ), cos(2* t )] at the point where t = pi/4.

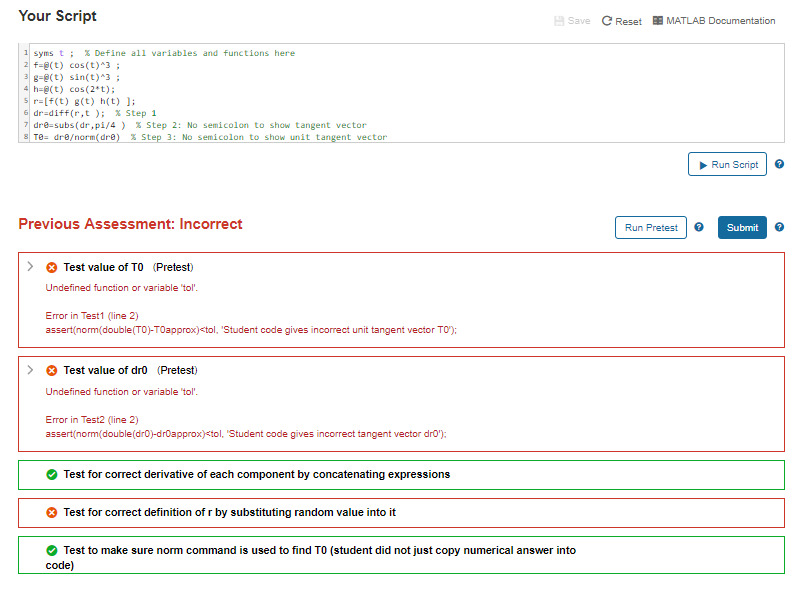
Your Script Save C Reset MATLAB Documentation syms t ; % Define all variables and functions here f-e(t) cos(t)3 8-8(t) sin(t)*3 h-(t) cos(2*t) r[(t) (t) h(t) J dr-diff(r,t ); % step 1 dre-subs(dr,pi/4 ) % Step 2: No semicolon to show tangent vector T8-dreorm( dre) % Step 3: No semicolon to show unit ta nt vector Run Script ) Previous Assessment: Incorrect Run Pretest Submit Test value of TO (Pretest) Undefined function or variable 'tol Error in Test1 line 2) assert norm(double(TO)-TOapprox)ctol, "Student code gives incorrect unit tangent vector TO); Test value of dr0 (Pretest) Undefined function or variable 'tol Error in Test2 (line 2) assert(norm(double(dr0)-droapprox)ctol, "Student code gives incorrect tangent vector drO); Test for correct derivative of each component by concatenating expressions Test for correct definition of r by substituting random value into it Test to make sure norm command is used to find TO (student did not just copy numerical answer into code)