First drop down options are less,the same, more.

Second is rise, fall.

The rest are numbers

idk what else you need these the answer options though

drop down 3 (1.5,1,0.7,2)

dd4 (1,-1,0.2,0.04)

dd5 (1.25,2.1,1.7,1.5)

dd6 (0.875,-0.625,1.625,0.35)

that is all the information given ...

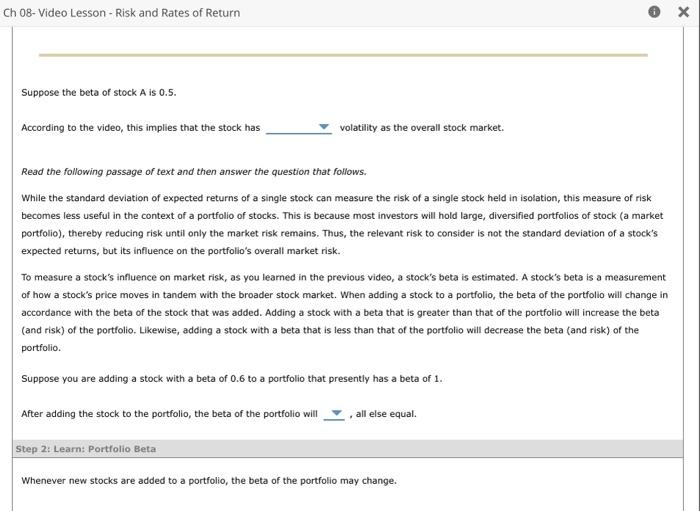
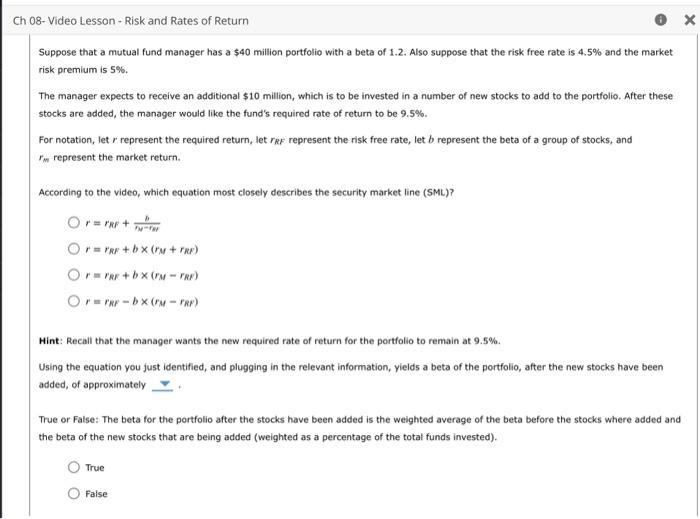
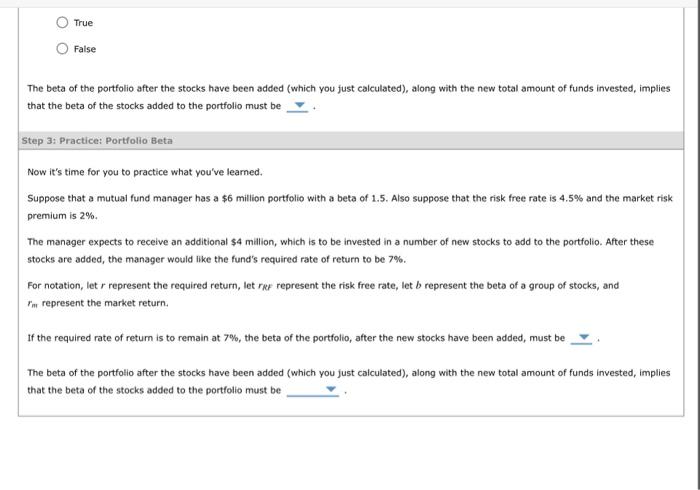
Suppose the beta of stock A is 0.5 . According to the video, this implies that the stock has volatility as the overall stock market. Read the following passage of text and then answer the question that follows. While the standard deviation of expected returns of a single stock can measure the risk of a single stock held in isolation, this measure of risk. becomes less useful in the context of a portfolio of stocks. This is because most investors will hold large, diversified portfolios of stock (a market portfolio), thereby reducing risk until only the market risk remains. Thus, the relevant risk to consider is not the standard deviation of a stock's expected returns, but its influence on the portfolio's overall market risk. To measure a stock's influence on market risk, as you learned in the previous video, a stock's beta is estimated. A stock's beta is a measurement of how a stock's price moves in tandem with the broader stock market. When adding a stock to a portfolio, the beta of the portfolio will change in accordance with the beta of the stock that was added. Adding a stock with a beta that is greater than that of the portfolio will increase the beta (and risk) of the portfolio. Likewise, adding a stock with a beta that is less than that of the portfolio will decrease the beta (and risk) of the portfolio. Suppose you are adding a stock with a beta of 0.6 to a portfolio that presently has a beta of 1. After adding the stock to the portfolio, the beta of the portfolio will , all else equal. Step 2: Learn: Portfolio Beta Suppose that a mutual fund manager has a $40 million portfolio with a beta of 1.2 . Also suppose that the risk free rate is 4.5% and the market risk premium is 5%. The manager expects to receive an additional $10 million, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 9.5%. For notation, let r represent the required return, let rRF represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. According to the video, which equation most closely describes the security market line (SML)? r=rRF+rMrMbr=rRF+b(rM+rRF)r=rRE+b(rMrRF)r=rRFb(rMrRE) Hint: Recall that the manager wants the new required rate of return for the portfolio to remain at 9.5%. Using the equation you just identified, and plugging in the relevant information, yields a beta of the portfolio, after the new stocks have been added, of approximately True or False: The beta for the portfolio after the stocks have been added is the weighted average of the beta before the stocks where added and the beta of the new stocks that are being added (weighted as a percentage of the total funds invested). True False True False The beta of the portfolio after the stocks have been added (which you just calculated), along with the new total amount of funds invested, implies that the beta of the stocks added to the portfolio must be Step 3: Practice: Portfolio Beta Now it's time for you to practice what you've learned. Suppose that a mutual fund manager has a $6 million portfolio with a beta of 1.5 . Also suppose that the risk free rate is 4.5% and the market risk premium is 2% The manager expects to receive an additional $4 milion, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 7%. For notation, let r represent the required return, let rk represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. If the required rate of retum is to remain at 7%, the beta of the portfolio, after the new stocks have been added, must be The beta of the portfolio after the stocks have been added (which you just caiculated), along with the new total amount of funds invested, implies that the beta of the stocks added to the portfolio must be Suppose the beta of stock A is 0.5 . According to the video, this implies that the stock has volatility as the overall stock market. Read the following passage of text and then answer the question that follows. While the standard deviation of expected returns of a single stock can measure the risk of a single stock held in isolation, this measure of risk. becomes less useful in the context of a portfolio of stocks. This is because most investors will hold large, diversified portfolios of stock (a market portfolio), thereby reducing risk until only the market risk remains. Thus, the relevant risk to consider is not the standard deviation of a stock's expected returns, but its influence on the portfolio's overall market risk. To measure a stock's influence on market risk, as you learned in the previous video, a stock's beta is estimated. A stock's beta is a measurement of how a stock's price moves in tandem with the broader stock market. When adding a stock to a portfolio, the beta of the portfolio will change in accordance with the beta of the stock that was added. Adding a stock with a beta that is greater than that of the portfolio will increase the beta (and risk) of the portfolio. Likewise, adding a stock with a beta that is less than that of the portfolio will decrease the beta (and risk) of the portfolio. Suppose you are adding a stock with a beta of 0.6 to a portfolio that presently has a beta of 1. After adding the stock to the portfolio, the beta of the portfolio will , all else equal. Step 2: Learn: Portfolio Beta Suppose that a mutual fund manager has a $40 million portfolio with a beta of 1.2 . Also suppose that the risk free rate is 4.5% and the market risk premium is 5%. The manager expects to receive an additional $10 million, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 9.5%. For notation, let r represent the required return, let rRF represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. According to the video, which equation most closely describes the security market line (SML)? r=rRF+rMrMbr=rRF+b(rM+rRF)r=rRE+b(rMrRF)r=rRFb(rMrRE) Hint: Recall that the manager wants the new required rate of return for the portfolio to remain at 9.5%. Using the equation you just identified, and plugging in the relevant information, yields a beta of the portfolio, after the new stocks have been added, of approximately True or False: The beta for the portfolio after the stocks have been added is the weighted average of the beta before the stocks where added and the beta of the new stocks that are being added (weighted as a percentage of the total funds invested). True False True False The beta of the portfolio after the stocks have been added (which you just calculated), along with the new total amount of funds invested, implies that the beta of the stocks added to the portfolio must be Step 3: Practice: Portfolio Beta Now it's time for you to practice what you've learned. Suppose that a mutual fund manager has a $6 million portfolio with a beta of 1.5 . Also suppose that the risk free rate is 4.5% and the market risk premium is 2% The manager expects to receive an additional $4 milion, which is to be invested in a number of new stocks to add to the portfolio. After these stocks are added, the manager would like the fund's required rate of return to be 7%. For notation, let r represent the required return, let rk represent the risk free rate, let b represent the beta of a group of stocks, and rm represent the market return. If the required rate of retum is to remain at 7%, the beta of the portfolio, after the new stocks have been added, must be The beta of the portfolio after the stocks have been added (which you just caiculated), along with the new total amount of funds invested, implies that the beta of the stocks added to the portfolio must be