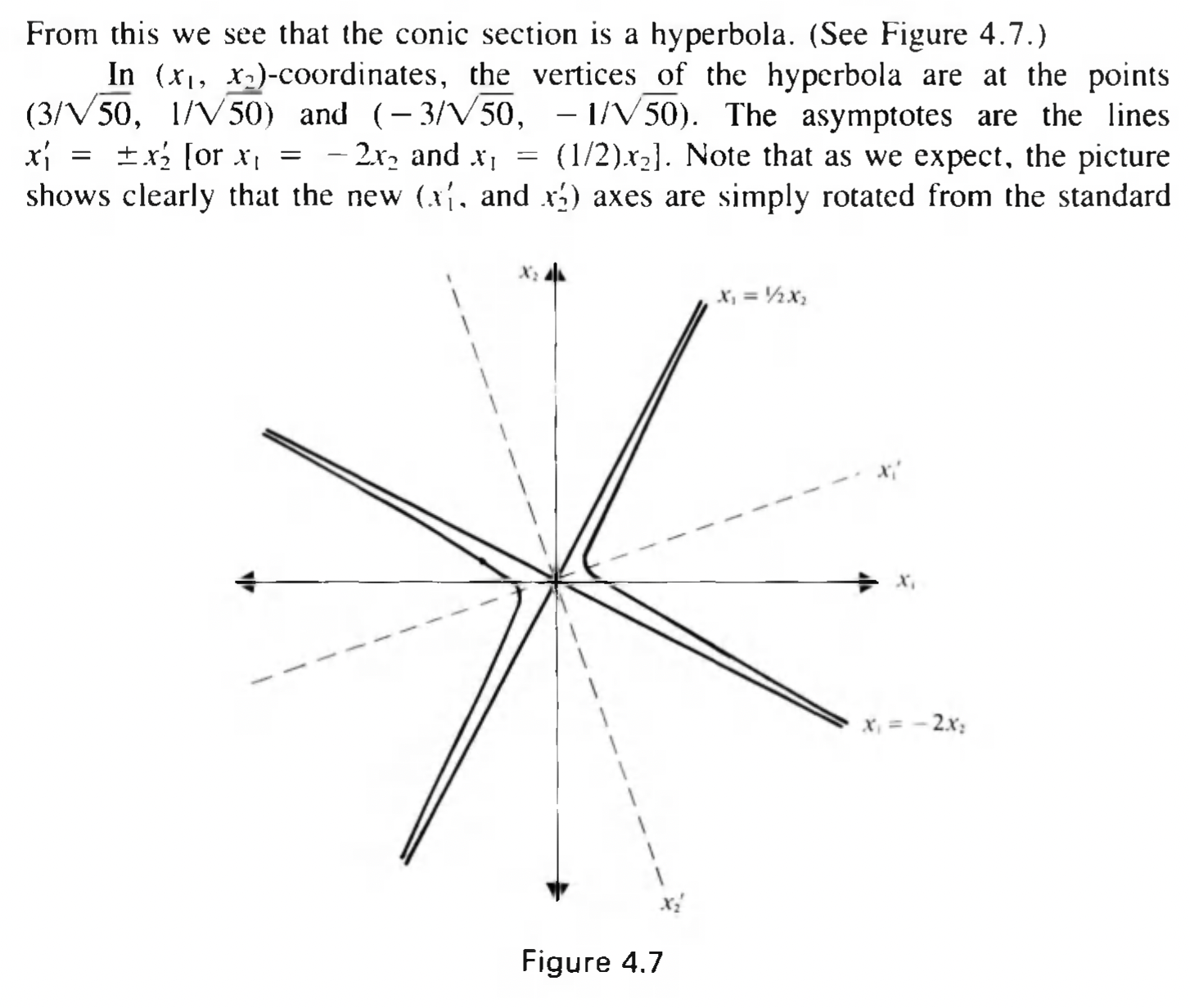
Question: First read example 4.6.5. from the Damiano and Little text. From this we see that the conic section is a hyperbola. (See Figure 4.7.) In
First read example 4.6.5. from the Damiano and Little text.

Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


