Question: First, we solve the problem by implementing it in Excel using the 2-dimensional matrix representation in worksheet 'Max flow'. J17 X Vfx A B D

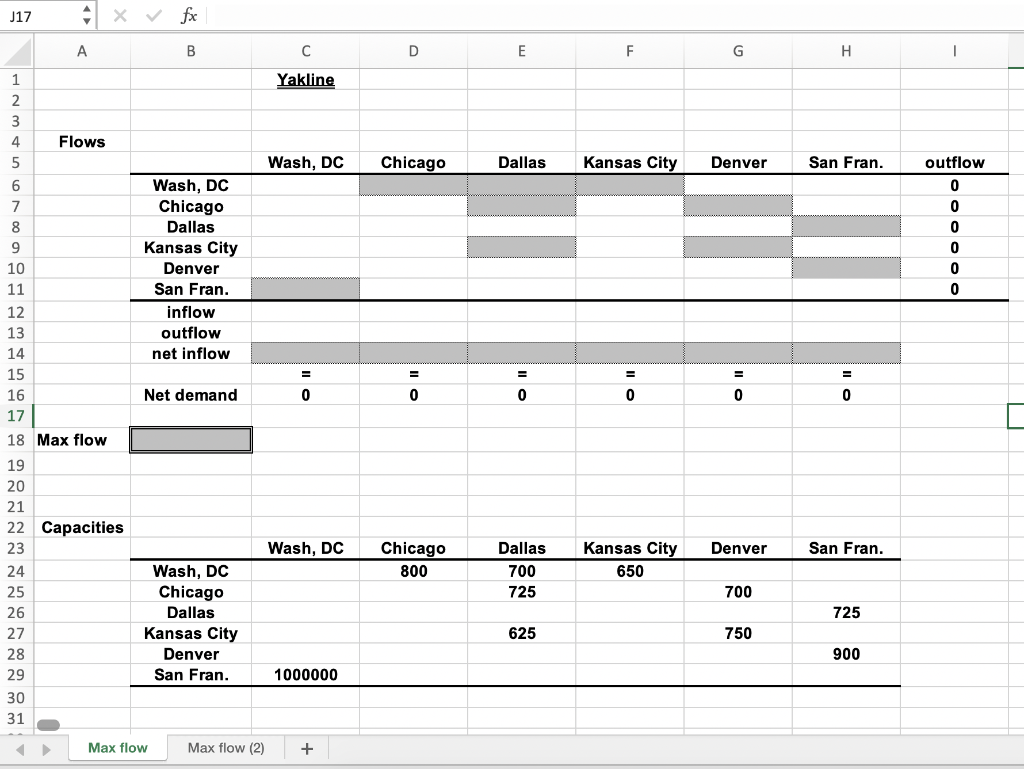
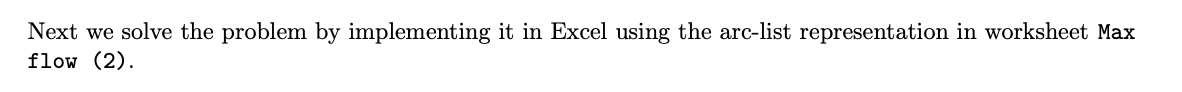
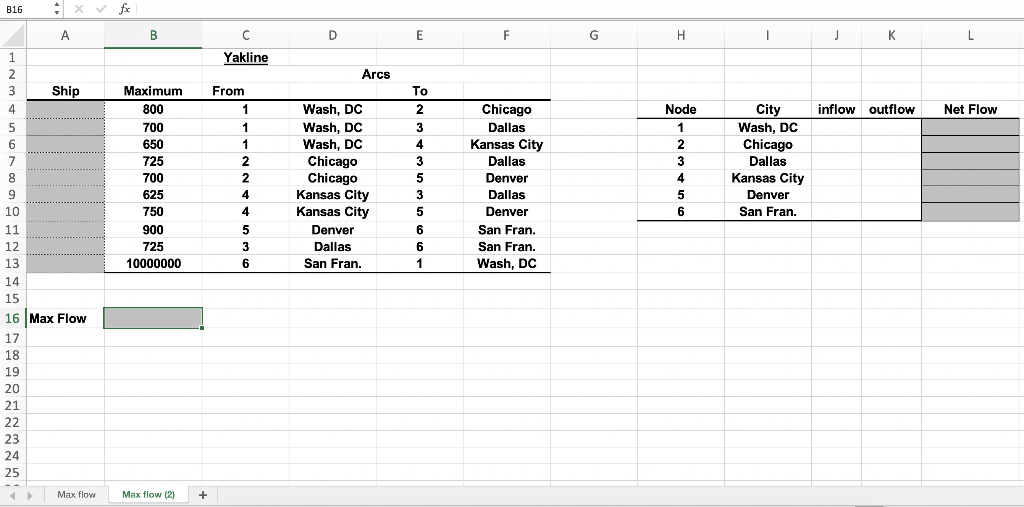
First, we solve the problem by implementing it in

First, we solve the problem by implementing it in Excel using the 2-dimensional matrix representation in worksheet 'Max flow'. J17 X Vfx A B D - E F G H Yakline 2 3 4 Flows 5 Wash, DC Chicago Dallas Kansas City Denver San Fran. 6 7 8 outflow 0 0 0 0 9 Wash, DC Chicago Dallas Kansas City Denver San Fran. inflow outflow net inflow 0 0 = = = = = Net demand 0 0 0 0 0 0 0 10 11 12 13 14 15 16 17 18 Max flow 19 20 21 22 Capacities 23 24 25 26 27 28 29 30 31 Wash, DC Denver San Fran. Chicago 800 Dallas 700 725 Kansas City 650 700 725 Wash, DC Chicago Dallas Kansas City Denver San Fran. 625 750 900 1000000 Max flow Max flow (2) + 22. Complete the Excel implementation in worksheet Max flow', solve the problem using Solver, and generate the sensitivity report. 23. Write down the Excel formula that goes in cell B18 of worksheet Max flow'. 24. Write down the Solver constraint formula that restricts each arc flow to be at most its capacity. 25. Is the optimal solution unique? Next we solve the problem by implementing it in Excel using the arc-list representation in worksheet Max flow (2). B16 fx B C D E F G H - J L K Yakline 1 2 3 Arcs Ship From To 4 1 2 Node inflow outflow Net Flow 1 5 6 1 1 2 2 3 7 Maximum 800 700 650 725 700 625 750 900 725 10000000 8 9 10 4 Wash, DC Wash, DC Wash, DC Chicago Chicago Kansas City Kansas City Denver Dallas San Fran. City Wash, DC Chicago Dallas Kansas City Denver San Fran. 2 4 4 3 4 3 5 3 5 6 6 1 Chicago Dallas Kansas City Dallas Denver Dallas Denver San Fran. San Fran. Wash. DC 5 6 5 3 6 11 12. 13 14 15 16 Max Flow 17 18 19 20 21 22 23 24 25 Max flow Max flow (2) + 26. Complete the Excel implementation in worksheet Max flow (2)' and solve the problem using Solver. 27. Write down the Excel formula that goes in cell J6 of worksheet Max flow (2). 28. Write down the Excel formula that goes in cell K9 of worksheet Max flow (2)'. 29. The optimal objective value is 1,625,000 calls. What is the lowest capacity (in 1,000s) for the segment between Washington DC and Kansas City that still allows to attain this maximum solution? First, we solve the problem by implementing it in Excel using the 2-dimensional matrix representation in worksheet 'Max flow'. J17 X Vfx A B D - E F G H Yakline 2 3 4 Flows 5 Wash, DC Chicago Dallas Kansas City Denver San Fran. 6 7 8 outflow 0 0 0 0 9 Wash, DC Chicago Dallas Kansas City Denver San Fran. inflow outflow net inflow 0 0 = = = = = Net demand 0 0 0 0 0 0 0 10 11 12 13 14 15 16 17 18 Max flow 19 20 21 22 Capacities 23 24 25 26 27 28 29 30 31 Wash, DC Denver San Fran. Chicago 800 Dallas 700 725 Kansas City 650 700 725 Wash, DC Chicago Dallas Kansas City Denver San Fran. 625 750 900 1000000 Max flow Max flow (2) + 22. Complete the Excel implementation in worksheet Max flow', solve the problem using Solver, and generate the sensitivity report. 23. Write down the Excel formula that goes in cell B18 of worksheet Max flow'. 24. Write down the Solver constraint formula that restricts each arc flow to be at most its capacity. 25. Is the optimal solution unique? Next we solve the problem by implementing it in Excel using the arc-list representation in worksheet Max flow (2). B16 fx B C D E F G H - J L K Yakline 1 2 3 Arcs Ship From To 4 1 2 Node inflow outflow Net Flow 1 5 6 1 1 2 2 3 7 Maximum 800 700 650 725 700 625 750 900 725 10000000 8 9 10 4 Wash, DC Wash, DC Wash, DC Chicago Chicago Kansas City Kansas City Denver Dallas San Fran. City Wash, DC Chicago Dallas Kansas City Denver San Fran. 2 4 4 3 4 3 5 3 5 6 6 1 Chicago Dallas Kansas City Dallas Denver Dallas Denver San Fran. San Fran. Wash. DC 5 6 5 3 6 11 12. 13 14 15 16 Max Flow 17 18 19 20 21 22 23 24 25 Max flow Max flow (2) + 26. Complete the Excel implementation in worksheet Max flow (2)' and solve the problem using Solver. 27. Write down the Excel formula that goes in cell J6 of worksheet Max flow (2). 28. Write down the Excel formula that goes in cell K9 of worksheet Max flow (2)'. 29. The optimal objective value is 1,625,000 calls. What is the lowest capacity (in 1,000s) for the segment between Washington DC and Kansas City that still allows to attain this maximum solution

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related General Management Questions!

The next 8 questions refer to the following problem: This question refers to the 'maximum flow problem' in the slides of this week, and the associated worksheets in the Excel Spreadsheet HW 6 . xlsx...

Hi Erylee88, I would like to utilize your service again. Same format different questions. Please find attached document for your review. Let me know. Thank you, Sam...

Submitted to Management Science manuscript MS-0001-1922.65 Authors are encouraged to submit new papers to INFORMS journals by means of a style file template, which includes the journal title....

financial SUBDOMAINS: 325.4 COMMUNICATING EFFECTIVELY IN ORGANIZATIONS 326.1 MANAGING INTERNAL COST & CONTROLLING FINANCES 326.2 MANAGING CAPITAL & FINANCIAL ASSETS 326.4 MANAGING ENTERPRISE RISK &...

I have C++ code that is trying to solve building and implementing a sliding block problem. Here is the Assignment: Part 1 Sliding Brick Puzzle Many of you might have played one or another version of...

WELCOME SIX SIGMA BLACK BELT CLASS Week 2 Virtual Class The 'live' session will start at the top of the hour In the meantime you can try out your microphone and speakers, select 'Meeting' then 'Audio...

Background: To illustrate the applications of statistics to quality control, we will use an example from a Midwest pharmaceutical company that manufactures individual syringes with a self-contained,...

Could you give me a step by step solution on excel for it please!! It'll be a great help for my coming exams !!! will thumbs up You are free to collaborate together all you like and share...

Assume you go to buy a $23,000 car and are offered the following deals. For both deals you you have $4,000 of your own money you can apply towards your new car (down payment). Or a. $1,000 immediate...

Required Fill in the blanks (indicated by the alphabetic letters in parentheses) in the following financial statements. Assume the company started operations January 1, 2016, and all transactions...

A patent is good for: Group of answer choices 1 4 years from date granted 2 0 years from time of application lifetime of the inventor plus 2 1 years 1 7 years from date granted 1 0 0 years

Case Greenbuilders Pte Lid ("GPL") is a local construction company which specialises in providing bespoke Design and Build construction services for private residential homes that are designed to be...