Fit the brass middle material, using the heat transfer paste (reminder All the heat source and the heater sink middle parts is constructed of the same material which is brass).Open the water supply valve to start the water flowing. Switch on the heater and set to the desired Watt power.wait for the temperature to stabilize and then record T1 to T7.Repeat the test at one or more heater powers greater than 30 W.

If one repeat the procedure 1, without using the thermal paste in interchangeable middle section, can you explain how the less effective contact area (without the paste) affects the results? If one repeat the procedure 1, with low heater setting (for example 30 W) and with no cooling water flow, can you explain what you are expected to get?

Please answer all the questions

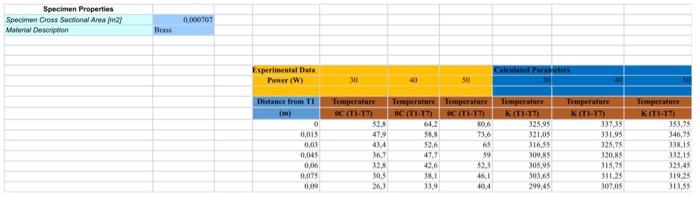
Specimen Properties Specimen Cross Sectional Area (m2) Material Desordion 0.000707 Brass Experimental Data Power (W) 50 Distance from TI () 0 0,015 Temperature C:17 Temperatur KT1-17) $23 47.9 0:03 Temperatur Temperature OCTI:17 CT17) 642 588 736 65 47,7 59 42.6 59 46.1 11,9 404 27 Temperature KT1-17 325,95 321.05 316.55 309,05 305,95 0765 299,45 Temperature K(T-17) 353,75 346,75 138,15 132.15 125.45 319.25 31335 0,045 0,06 331.95 325,75 320,NS 315,95 311,25 307,05 M. 123 10.5 26,1 O, From the results for each power setting, plot charts of temperature against distance along the bar, with respect to the first thermocouple (T1) (see example Figure 1). You should be able to draw a good best fit line through your results, as all parts are of the same material. Calculate the thermal gradient of the line. Use the two readings Tz to T5, the given distance between them (L=0.03 m), the heater power, Q, and the cross sectional area of the specimen (A=0.000707 m2), to calculate the thermal conductivity of each of the specimen. Compare it with the typical thermal conductivity value of the brass - search for the value through web. What do you notice about the gradient of the charts for each heater power setting? Specimen Properties Specimen Cross Sectional Area (m2) Material Desordion 0.000707 Brass Experimental Data Power (W) 50 Distance from TI () 0 0,015 Temperature C:17 Temperatur KT1-17) $23 47.9 0:03 Temperatur Temperature OCTI:17 CT17) 642 588 736 65 47,7 59 42.6 59 46.1 11,9 404 27 Temperature KT1-17 325,95 321.05 316.55 309,05 305,95 0765 299,45 Temperature K(T-17) 353,75 346,75 138,15 132.15 125.45 319.25 31335 0,045 0,06 331.95 325,75 320,NS 315,95 311,25 307,05 M. 123 10.5 26,1 O, From the results for each power setting, plot charts of temperature against distance along the bar, with respect to the first thermocouple (T1) (see example Figure 1). You should be able to draw a good best fit line through your results, as all parts are of the same material. Calculate the thermal gradient of the line. Use the two readings Tz to T5, the given distance between them (L=0.03 m), the heater power, Q, and the cross sectional area of the specimen (A=0.000707 m2), to calculate the thermal conductivity of each of the specimen. Compare it with the typical thermal conductivity value of the brass - search for the value through web. What do you notice about the gradient of the charts for each heater power setting