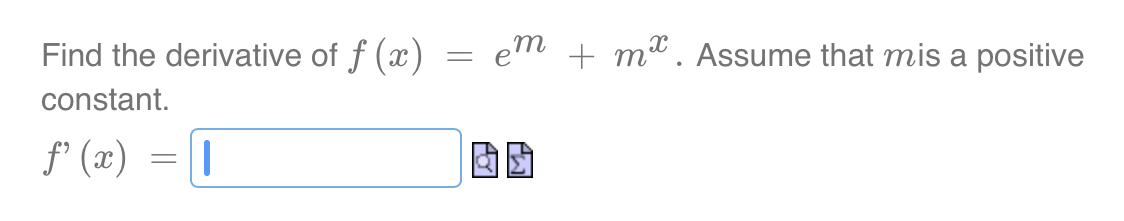
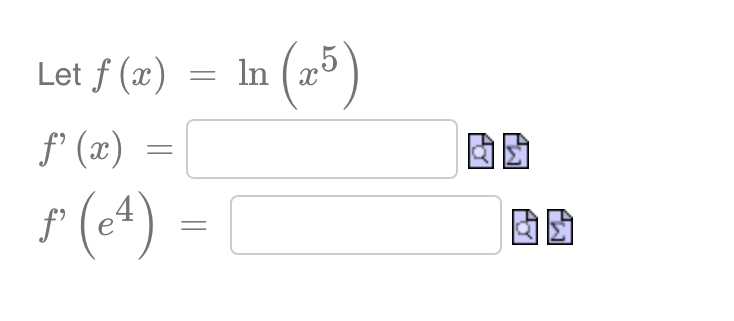
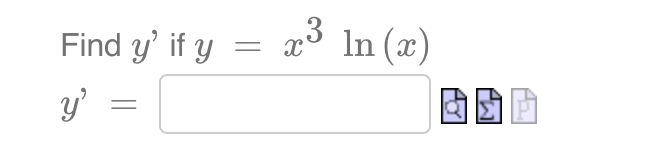
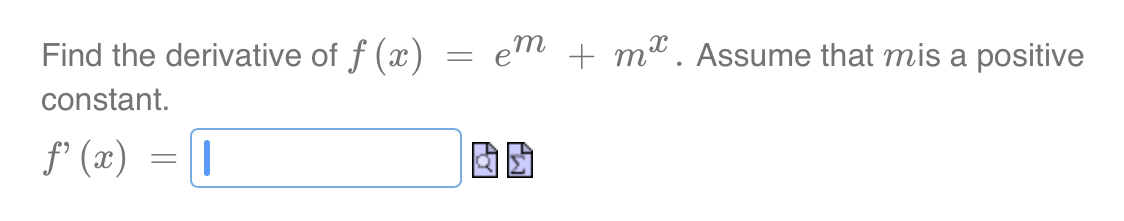
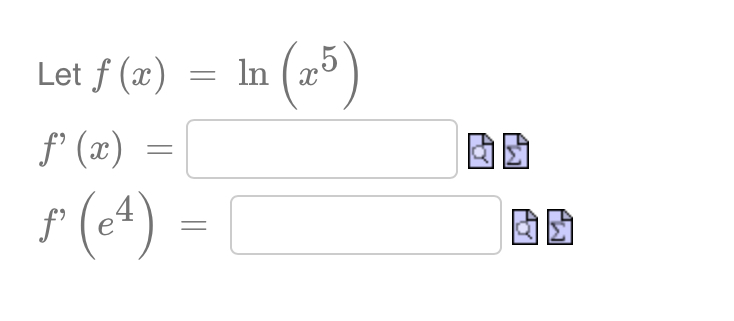
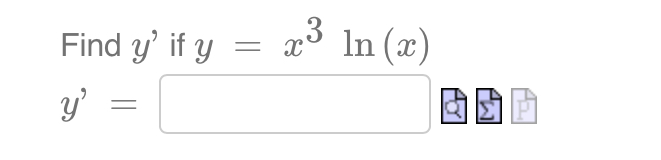
\fLet f (ac) = In 5 f' (ac) = E f' ( e4 ) = EIf the radius of a sphere is increasing at a constant rate of 3 cm/seccm/sec, then the volume is increasing at a rate of Number cm3 / sec when the radius is 4cm. aging 3 dt d'r dt ' Hint: and the volume of a sphere is V 2 gm\" 3 Find the derivative of f (ac) = 202 + 203. f' (ac )\fA spotlight on the ground is shining on a wall 16m away. If a woman 2m tall walks from the spotlight toward the building at a speed of 0.6m/s, how fast is the length of her shadow on the building decreasing when she is 4m from the building? Answer (in meters per second): Number