Flow Condition #$1$: When studying uniform flow we learned how to calculate the normal depth, $y_n$ for a given combination of discharge $Q,$ bottom slope $S_0,$ channel geometry, and roughness. In the uniform flow lab we saw how the flow tended to become uniform in the $60$ foot long flume, for $Q=1\mathrm{.}4cfs,S_0=2\mathrm{.}6{10}^{-4}.$ The relatively long prismatic channel determined the depth$-$discharge relationship, thus "controlling" the flow and producing a subcritical uniform flow with $y_n=0\mathrm{.}50ft($how would you verify that the flow was subcritical?$).$

In this flow condition a sluice gate that controls the flow from the head tank into the flume was introduced, otherwise keeping $Q$ and $S_0$ constant. This additional "control" produces at the upstream end of the flume a supercritical flow with depth $).$ The flow varies rapidly from supercritical to subcritical, forming a hydraulic jump a short distance downstream of the gate. The flow depth upstream of the jump, $y_1,$ is practically equal to the opening under the gate.

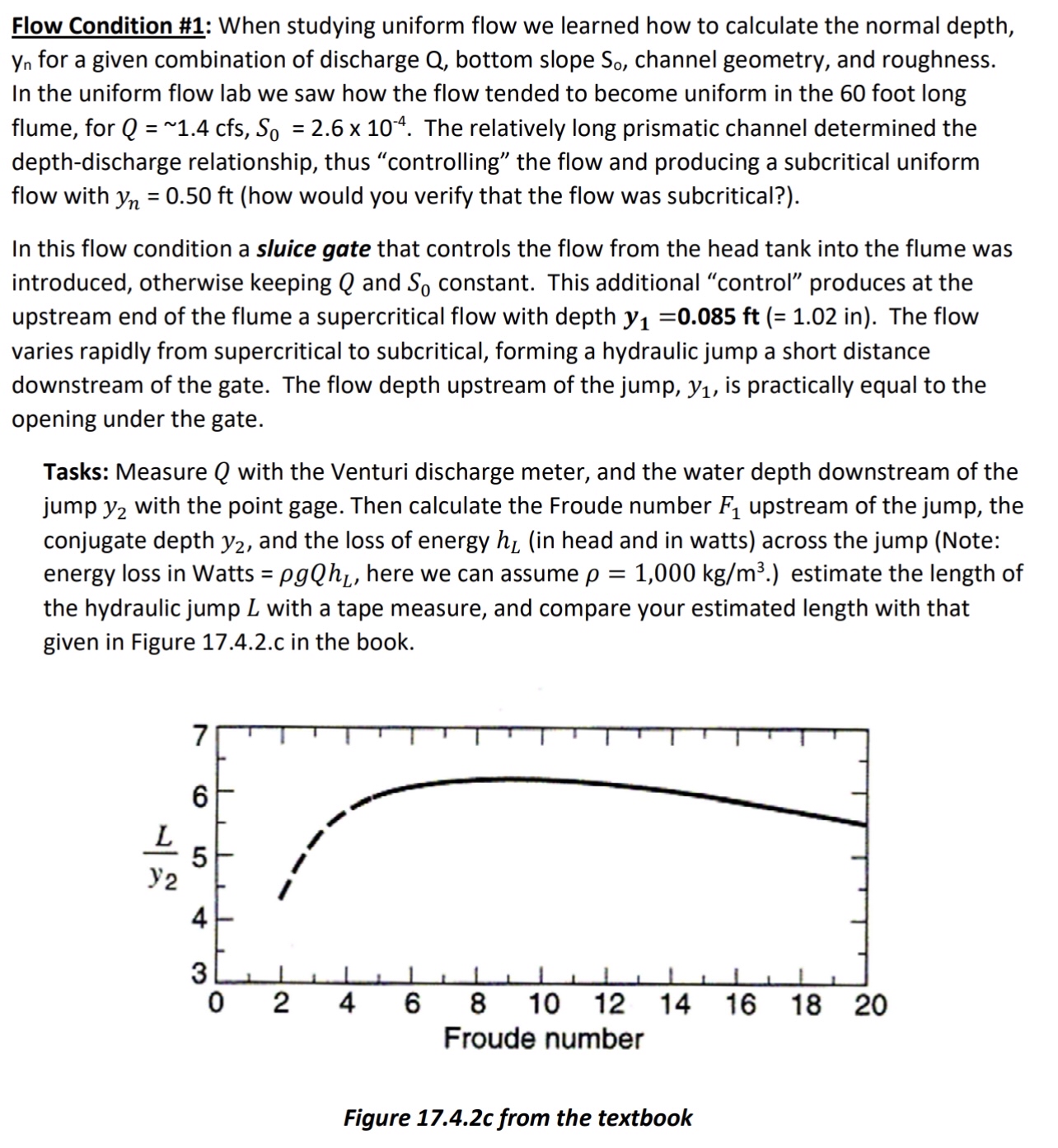
Tasks: Measure $Q$ with the Venturi discharge meter, and the water depth downstream of the jump $y_2$ with the point gage. Then calculate the Froude number $F_1$ upstream of the jump, the conjugate depth $y_2,$ and the loss of energy $h_L($in head and in watts$)$ across the jump $($Note: energy loss in Watts $=gQ{h}_L,$ here we can assume $=1,000k\frac{g}{m^3}.)$ estimate the length of the hydraulic jump $L$ with a tape measure, and compare your estimated length with that given in Figure $17\mathrm{.}4\mathrm{.}2.$c in the book.

Figure $17\mathrm{.}4\mathrm{.}2$c from the textbook