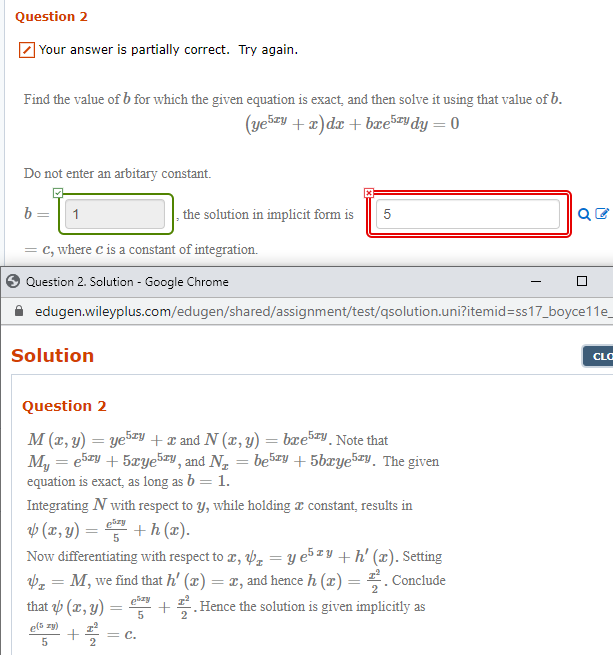
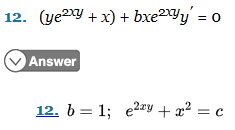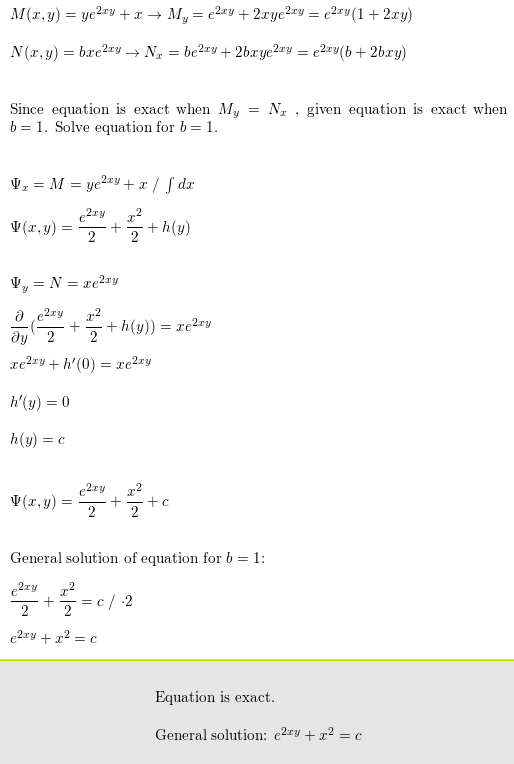Question: fM(x, y) = yelTy + x - My = ely + 2xyely = ezzy(1 + 2ry) N(x, y) = brelry - NI = belry +
\fM(x, y) = yelTy + x - My = ely + 2xyely = ezzy(1 + 2ry) N(x, y) = brelry - NI = belry + 2brye2ry = e2ry(b + 2bry) Since equation is exact when My = Nx , given equation is exact when b = 1. Solve equation for b = 1. VI = M = yezzy + x / Jdx V(x,y) = 2 + +h(y) Vy = N = celly au 2 + -+h(y)) = celry celTV + h'(0) = relay h'(y) =0 h(y) = c 2 + +c General solution of equation for b = 1: 2 + = c/ -2 Equation is exact. General solution: e2x# + x2 = c1 We first find M, and Ny and set them equal to each We recognise that M(x, y) = years and N(x,y) = other. By factoring it's easy to see that we need to bre2ry, so set b = 1. We choose an arbitrary y derivative and integrate. My = 2rye2ry + eloy = elv(1 + 2xy) For this problem I personally found it easier to integrate and We then find the derivative of that in terms of r so that we could compare it to the r derivative of v, N, = 2brye2 + belly = be2"#(1 + 2xy). VI. We find r to be what is needed to make the equality thus b = 1. make sense, and plug back into the integrated vy We now need to find a w where v. = years and (which is supposed to be a "draft" version of what why = re2ry. We see that should be) to find the completed y function. 1 2x8 + h(2) where h(x) is some arbitrary function of r. We calculate and setting that equal to vr yields h'(r) = r, so h(I) = , +c, for some constant c. Thus we find (x,y) = e- + x- = c. RESULT (x,y ) = ely + 1' = c.Consider the differential equation as follows: (yet + x) dx+bxe?"dy=0. The objective is to determine the value of b for which the differential equation is exact and then to solve the equation using that value of b. Comment Step 2 of 4 A Recall the concept of exact differential equation as follows: A differential equation of the form Mix + Ady =0 is said to be exact if M. = N. Here, M and / are the functions of x and y and M and /V, represents the first order partial derivative of M and / respectively with respect to y and x respectively. Compare the given differential equation (yet + x)dx+ bxe "dy =0 with standard form of equation Mdx + Ndy =0. This implies as follows: M(x, y) = (vel+x) N(x,y ) = brew Solve the first order partial derivative of M with respect to y and partial derivative of / with respect to x. M(x, y) = (vel+x) , = 2 (vezv +x) =elv + 2xyev +0 { By product rule on first term) =elv +2xvel N(x, y) = bxe N. = (brew ) ar = be?" + 2bxve For the differential equation to be exact, M, (x, y) = N, (x, y ) elv + 2xyel" = be*+2xybev ely - be's + 2xyel -2bxyel* =0 ew (1-b)+2xyew (1-b)=0 b=1 Hence, the required value of b for which the differential equation is exact is b = 1Step 3 of 4 A Substitute the value /=1 in the differential equation. The differential equation becomes (yet + x)dr+ xevdy =0. Compare with standard form of differential equation. This implies M = ye " + x and N=xew. Since the differential equation is exact then there is a function o (x. y )such that w (x, y) = M (x, y) and w, (x, y) = N(x,y) Integrating the first of the above equations. W. (x, y ) = M(x, y ) W. (x. y) = yev+x As M(x. v) = vel+x) w(xy)= [(vel+x)dx ( Integrate with respect to x treating y as constant) 2x 2 -+h(y) w (x, y) = 2 -th(y) 2 Partially differentiate above equation with respect to y. w(x,v)= Ith(y) 2 2 w, (x,y)=2x+0 +W'(y) = xew +h(y) By condition (1). w, (x, y ) = N (x,y) xe " + h (y) =xe (Substitute respective values} "(y ) =0 This further implies that h()) =0 as the constant of integration can be omitted because any solution is satisfactory.Step 4 of 4 Substitute the value h (y) =0 in function w (x, y)= X + th(y) 2 hJ This implies that the solution of differential equation is as follows: w ( x, y ) = k + =k 2 2 3+x = 2k (2k = C) Here, k and C are arbitrary constants. Hence, the required solution of the exact differential equation isQuestion 2 Your answer is partially correct. Try again. Find the value of 6 for which the given equation is exact, and then solve it using that value of b. (yeszy + x) da + brestudy = 0 Do not enter an arbitary constant. the solution in implicit form is 5 = C, where c is a constant of integration. Question 2. Solution - Google Chrome - 0 edugen.wileyplus.com/edugen/shared/assignment/test/qsolution.uni?itemid=ss17_boyce1 1e Solution CLO Question 2 M (x, y) = yebzy + x and N (x, y) = breazy. Note that My = eazy + 5xyeary, and Nx = bery + 5bayebry. The given equation is exact, as long as b = 1. Integrating /V with respect to y, while holding c constant, results in (x, y) = th(x). Now differentiating with respect to c, v, = yeszy + h' (x). Setting = M, we find that h' (x) = x, and hence h (c) = , . Conclude that o (c, y) = ebry 5 -+ . Hence the solution is given implicitly as e(5 zy) 5 2 C.Question 1 Find the value of 6 for which the given equation is exact, and then solve it using that value of b. (yebry + x) do + breydy = 0 Do not enter an arbitary constant. b = Number the solution in implicit form is QC = c, where C is a constant of integration