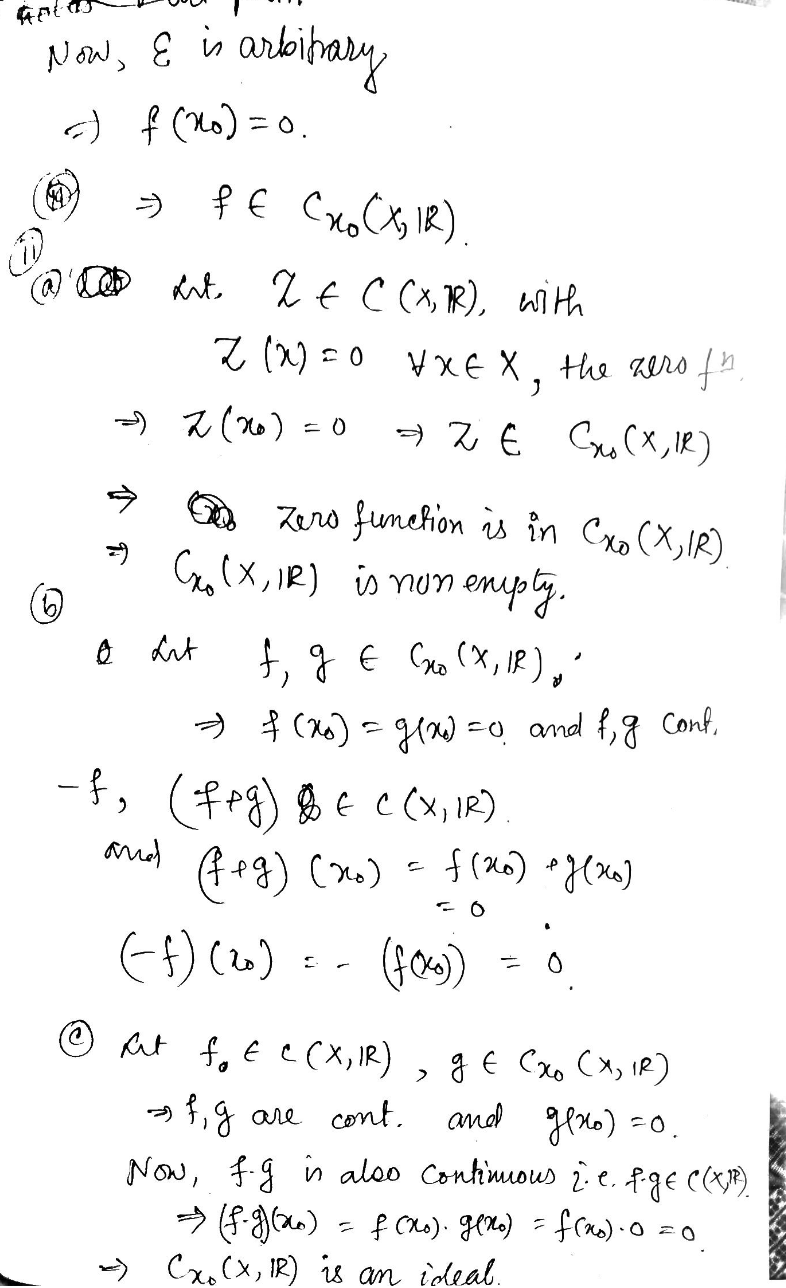
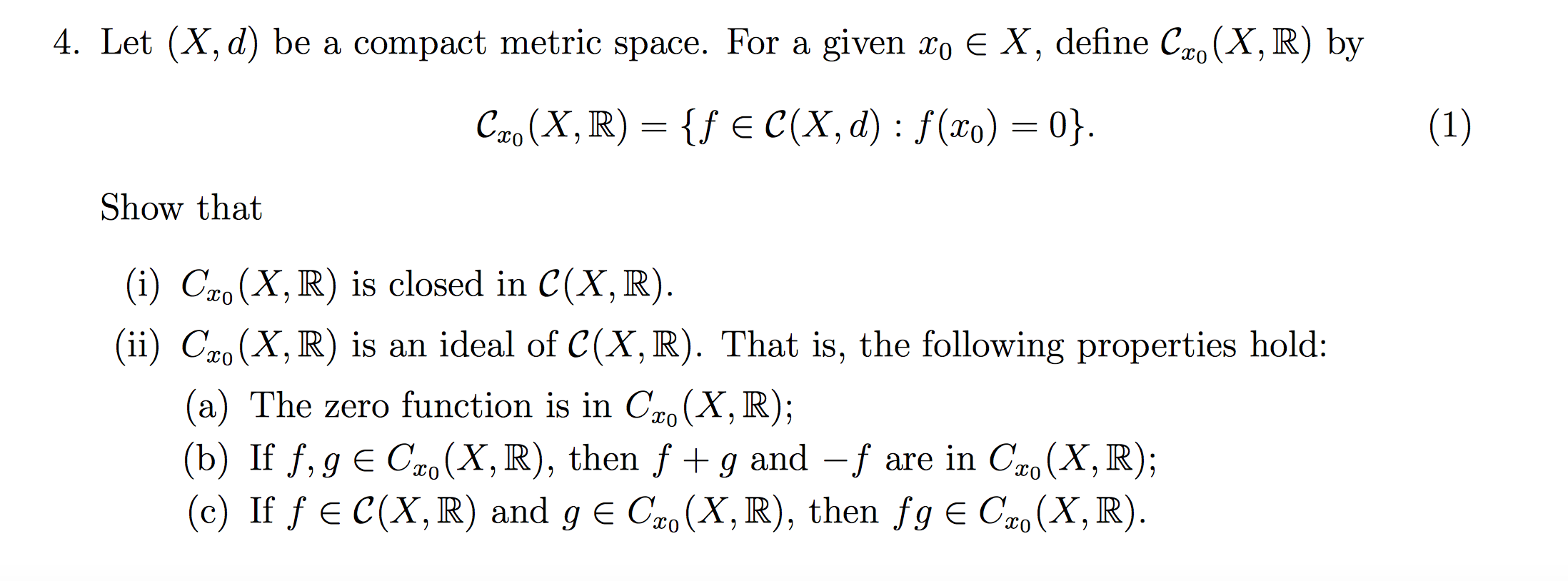
\fNow , E is arbitrary, .) f ( 20 ) = 0. 3 PE (x ( X, 1R ) int. RE C ( x, PR), with 2 ( x) =O VXEX . the zerofo. 2 ( 260 ) = 0 - 2 E Co ( X , IR ) So zero function is in Cxo (X, IR ) G (x, IR ) is nonempty. A dat f g E Co ( X , IR ) . ' 7 8 ( x0 ) = glo ) = 0 and f , g cont . - f , ( fpg ) & G C ( x , IR ) and (fig ) ( x10) = f (260 ) +g( x40 ) ( - f ) ( 20 ) = - (fox ) . At f. E c ( X, IR ), g f ( xo ( x , IR ) f ,g are cont . and fix60 ) =0 . Now, f.9 is also continuous ?e. Page ( ( X/P) - ( 8-9) ( 260 ) = F CXo ) . get ) = f (xo ) 0 =0 -) Cx. ( x, IR ) is an ideal .4. Let (X, d) be a compact metric space. For a given To E X, define Cro (X, R) by Cro (X, R) = {f EC(X, d) : f(x0) = 0}. (1) Show that (i) Cro (X, R) is closed in C(X, R). (ii) Cro (X, R) is an ideal of C(X, R). That is, the following properties hold: (a) The zero function is in Cro (X, R); (b) If f, g E Cro (X, R), then f + g and -f are in Cro (X, R); (c) If f EC(X, R) and g E Cro (X, R), then fg E Cro (X, R)