for a divergence theorem by cylindrical coordinates, I understand every steps but am so confused about how to find the boundary of theta. For example, question and answer like this, I don't understand why the boundary of theta is 0 to pi(1st question) and 0 to pi/2(2nd question) instead of 0 to 2pi. Could you please explain details about how to find the boundary of theta

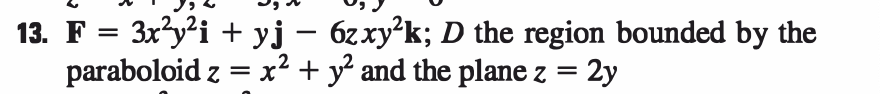
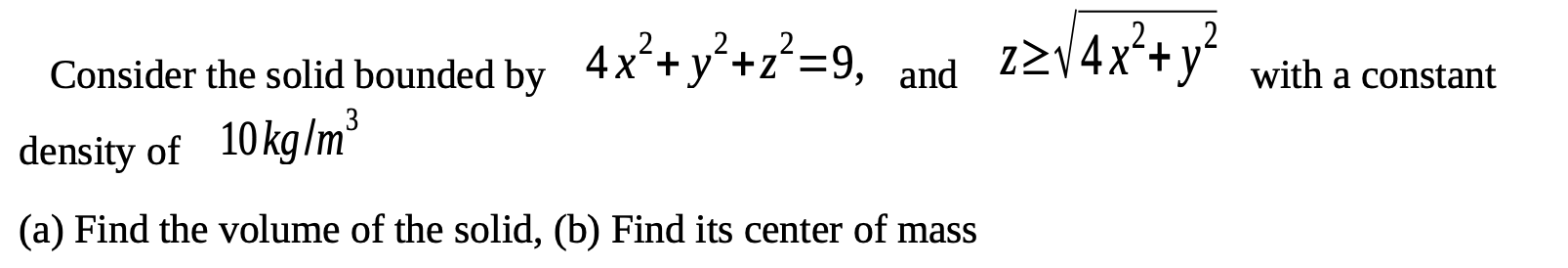
The region is bounded by z=x + y and the plane z= 2y. So, the limits of z varies from x + y to 2y. Thus, SS (F . n)ds = fff lav III, dadydx - If(=), dvdx ff (2y-x2 - y? )dvdx Convert it in to polar coordinates (x= rcos0, y = rsin0), 2sine If (F .n)ds = ] [ (2rsin0-r cos' 0-r sin Orderde 0=0 r=0 2sin0 = (2rsin0 -72 (cos' 0 + sin' @)ydrde 0=0 r=0 2sino = (2rsin 0-ra )arde 0-0 r=0 2sin0 (2r sin 0-r) )drde 0-0 r=0 1 2sino- 4 \\2sin 0 4 do 3 | 2sino (2sino) _(2sin0)_0 de 4 2 sin O (8sin' 0) 16sin* 0 de 020 3 's sin' 0- 16 sin' e de 16 16 3 4 [ sin* 0de 0=0 16 3 -4 [sin* 0de 0=0 16-12 x 2 sin* Ode 3 0=0 w / 0o sin* 0de 0-0 Use the reduction formula in integrals, [sin" Ode = _ cossin" 0 n-1 [ sin"-2 0do n Put n=4, [f(F.n)ds = 3 cos @sin #-10 4-1 [sin $ 2 0de13. F = 3x y i + yj - 6zxy k; D the region bounded by the paraboloid z = x2 + y and the plane z = 2y2 2 2 2 2 Consider the solid bounded by 4 X + y +2 :9: and Z 2J4 X +y with a constant 3 density of 10 kg I m (a) Find the volume of the solid, (b) Find its center of mass