For a given undirected, unweighted simple graph and a fixed positive integer $k,$ the $k-$coloring problem asks us to assign a color to each vertex, using at most $k$ different colors, such that no two adjacent vertices have the same color.

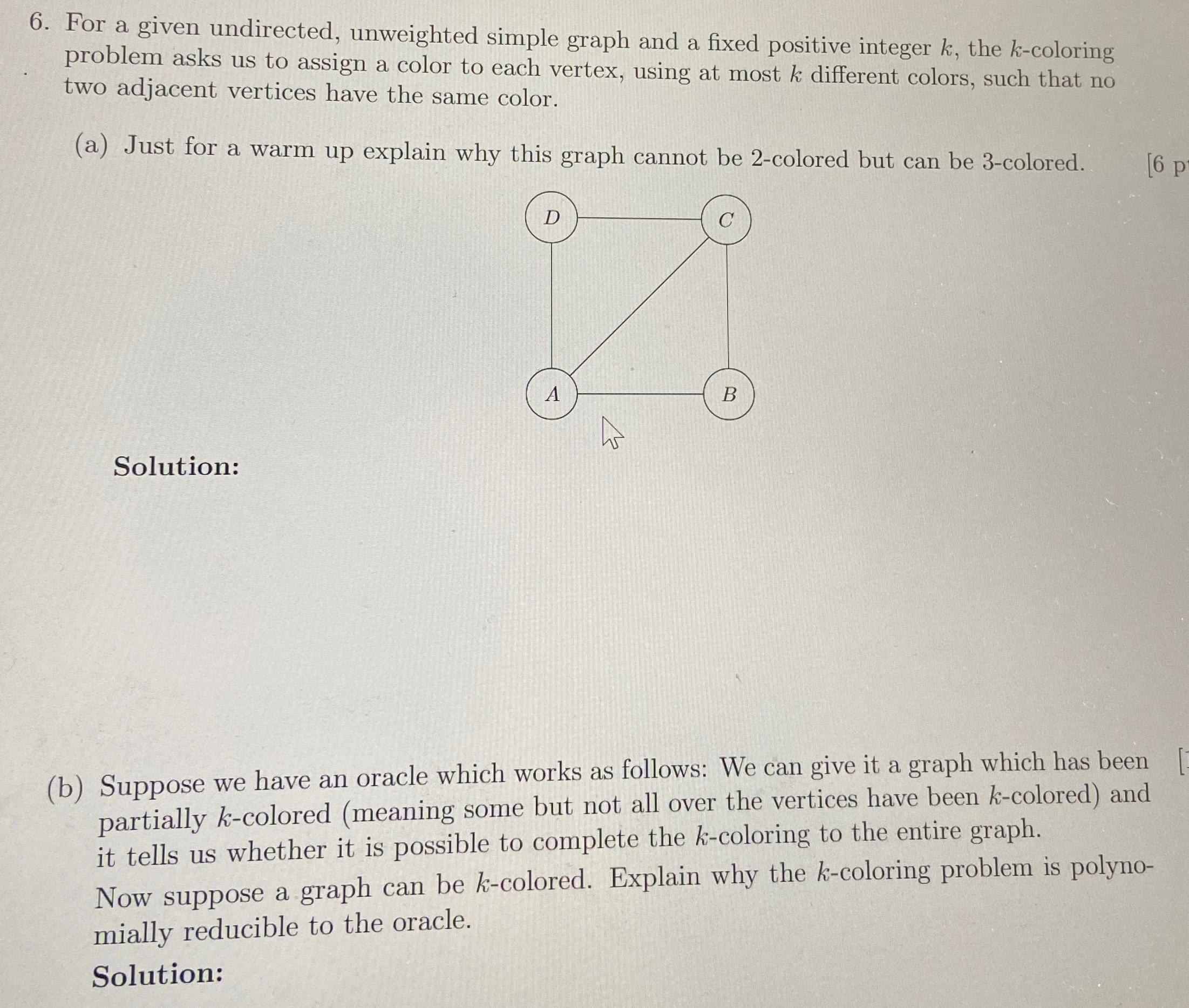
$($a$)$ Just for a warm up explain why this graph cannot be $2-$colored but can be $3-$colored.

Solution:

$($b$)$ Suppose we have an oracle which works as follows: We can give it a graph which has been partially $k-$colored $($meaning some but not all over the vertices have been $k-$colored$)$ and it tells us whether it is possible to complete the $k-$coloring to the entire graph. Now suppose a graph can be $k-$colored. Explain why the $k-$coloring problem is polynomially reducible to the oracle.

Solution: