For a spring$-$mass$-$damper system, $m=50kg$ and $k=500\frac{N}{m}.$ Find the following:

a$.$ The system critical damping constant, $c_c.$

b$.$ The system damped natural frequency when $c=c_c,$ and

c$.$ The system logarithmic decrement.

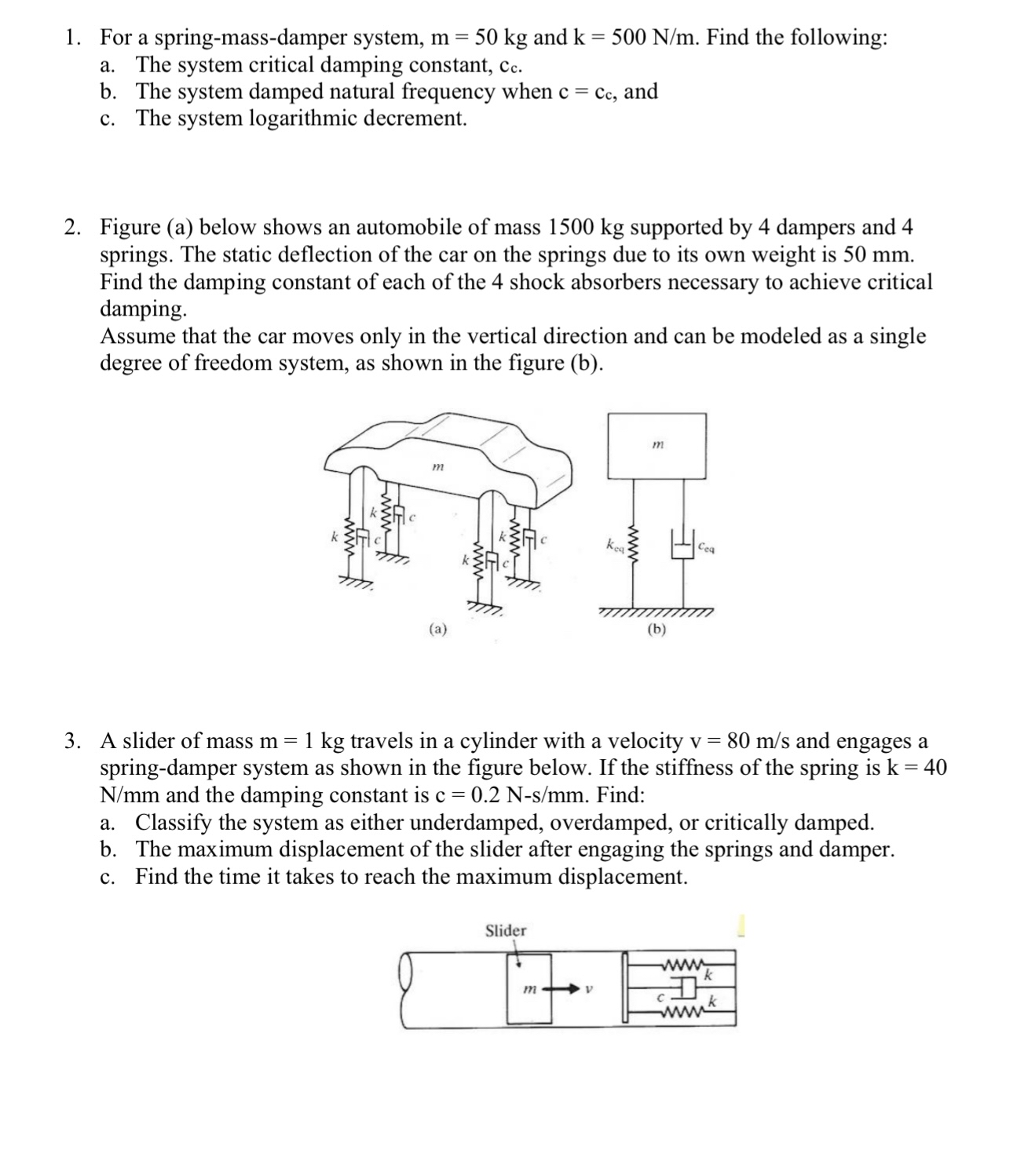
Figure $($a$)$ below shows an automobile of mass $1500$ kg supported by $4$ dampers and $4$

springs. The static deflection of the car on the springs due to its own weight is $50$ mm $.$

Find the damping constant of each of the $4$ shock absorbers necessary to achieve critical

damping.

Assume that the car moves only in the vertical direction and can be modeled as a single

degree of freedom system, as shown in the figure $($b$).$

A slider of mass $m=1kg$ travels in a cylinder with a velocity $v=80\frac{m}{s}$ and engages a

spring$-$damper system as shown in the figure below. If the stiffness of the spring is $k=40$

$\frac{N}{m}m$ and the damping constant is $c=0\mathrm{.}2N-\frac{s}{m}m.$ Find:

a$.$ Classify the system as either underdamped, overdamped, or critically damped.

b$.$ The maximum displacement of the slider after engaging the springs and damper.

c$.$ Find the time it takes to reach the maximum displacement.