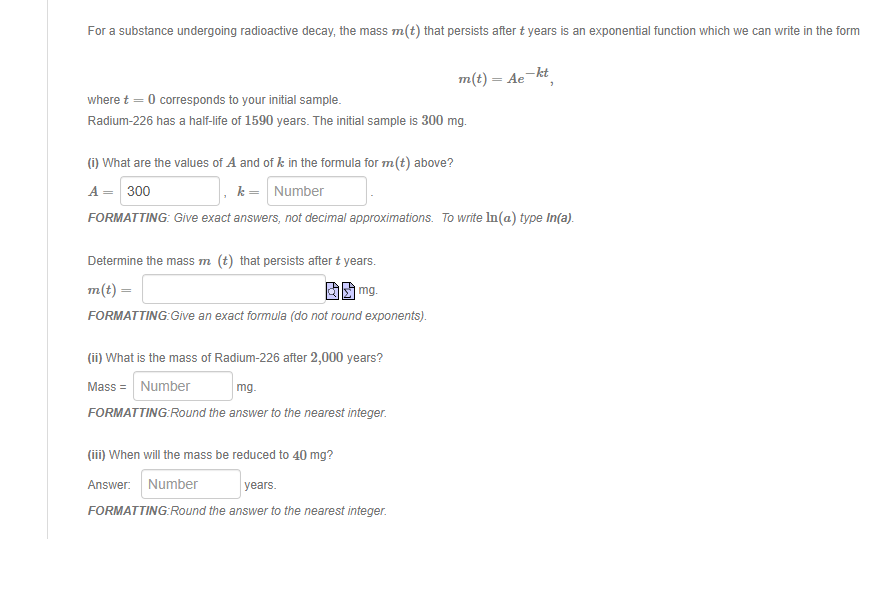
Question: For a substance undergoing radioactive decay, the mass ( boldsymbol { m } ( t ) ) that persists after (
For a substance undergoing radioactive decay, the mass boldsymbolmt that persists after t years is an exponential function which we can write in the form
mtA ek t
where t corresponds to your initial sample.
Radium has a halflife of years. The initial sample is mg
i What are the values of A and of boldsymbolk in the formula for boldsymbolmt above?
A
k
FORMATTING: Give exact answers, not decimal approximations. To write ln a type ln a
Determine the mass mt that persists after t years.
mt
mg
FORMATTING:Give an exact formula do not round exponents
ii What is the mass of Radium after years?
Mass mg
FORMATTING:Round the answer to the nearest integer.
iii When will the mass be reduced to mg
Answer: pears.
FORMATTING:Round the answer to the nearest integer.
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


