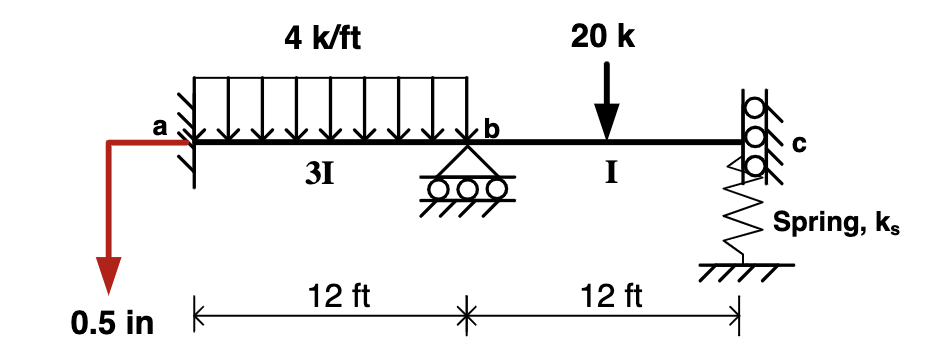
For all members:

E $=207360$ k$/$ft$2$

I $=1/12$ ft$4$

L $=12$ ft

Area: Aab $=0\mathrm{.}25$ ft$2$ and Abc $=0\mathrm{.}1$ ft$2$

Spring: ks $=8$EI$/$L$3$

Note: I and A is different for members AB and BC$,$ and concentrated force is applied at the center of the span.

For the beam shown in figure below, using the stiffness method, calculate all

the unknown nodal displacements and member forces in beams ab and bc$.$Temperature: Member AB has temperature change such that: Tu $=150\backslash$deg F$,$ Tl $=$

$0\backslash$deg F and Tc $=75\backslash$deg F$,$ Section is symmetric with height $=12$ in and alpha $=$

$6\mathrm{.}5\backslash$times $106$ ft$/($ft$\backslash$deg F$)$

Fabrication error: Member BC has out of straightness fabrication error Ebc $=0\mathrm{.}5$ in$.$

Support Settlement: The support A settles down by $0\mathrm{.}5$ in

Use a numbering system for each node instead of lettering system$-$ draw diagram to show numbers