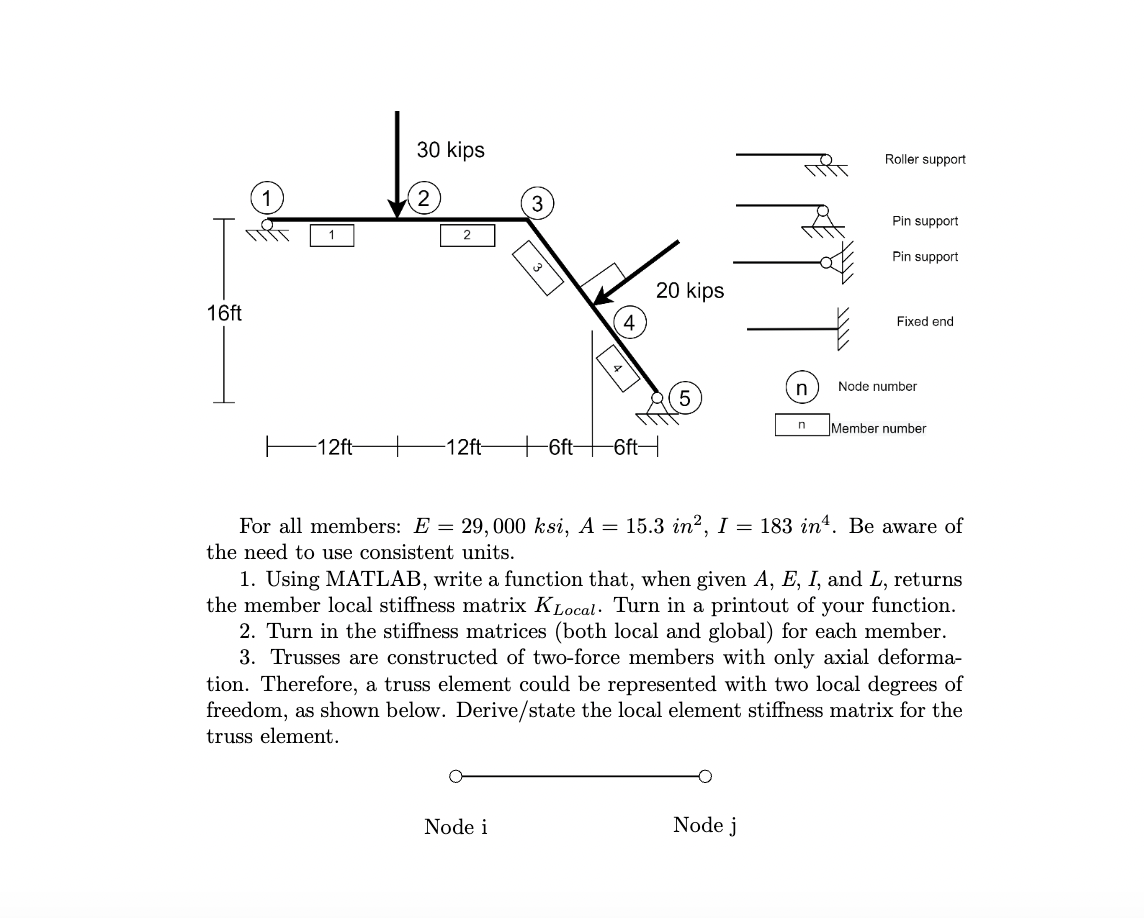
For all members: E$=29,000$ksi,A$=15\mathrm{.}3$in$^(2),$I$=183$in$^(4).$ Be aware of the need to use consistent units.

Using MATLAB, write a function that, when given A$,$E$,$I, and L$,$ returns the member local stiffness matrix K$\_($Local $).$ Turn in a printout of your function.

Turn in the stiffness matrices $($both local and global$)$ for each member.

Trusses are constructed of two$-$force members with only axial deformation. Therefore, a truss element could be represented with two local degrees of freedom, as shown below. Deriv$($e$)/($s$)$tate the local element stiffness matrix for the truss element.