For alphabet $,$ given languages $L_1$ and $L_2$ over $,$ the set$-$wise concatenation is defined as $L_1$

$L_2=\{\begin{array}{cc}\text{w}\text{i}\text{n}& {}^{**}|w=uv\end{array}$ for some strings $uin{L}_1$ and $\{$:$vin{L}_2\}$

Q$1\mathrm{.}1$

$1$ Point

Consider the alphabet $\{a,b\}.$ How many strings are in the set $\{,a,b\}$@$\{,a,b\}?$

$0($i$.$e$.$l the set is empty$)$

$3$

$6$

$9$

Some other $($finite$)$ number

Infinitely many unique strings

Q$1\mathrm{.}2$

$2$ Points

Let $N_1=(Q_1,,{}_1,q_1,F_1)$ and $N_2=(Q_2,,{}_2,q_2,F_2)$ be NFAs. When applying the

construction in Theorem $1\mathrm{.}47$ to build the NFA $N=(Q,,,q_1,F_2)$ that recognizes $L(N_1)$@

$L(N_2),$ select all and only the statements below that are universally true.

$\frac{?}{\text{b}\text{a}\text{r}}(|Q|)=|Q_1|+|Q_2|\frac{?}{b}$

$ar(|Q|)=|Q_1|*|Q_2|$

Q$1\mathrm{.}3$

$1$ Point

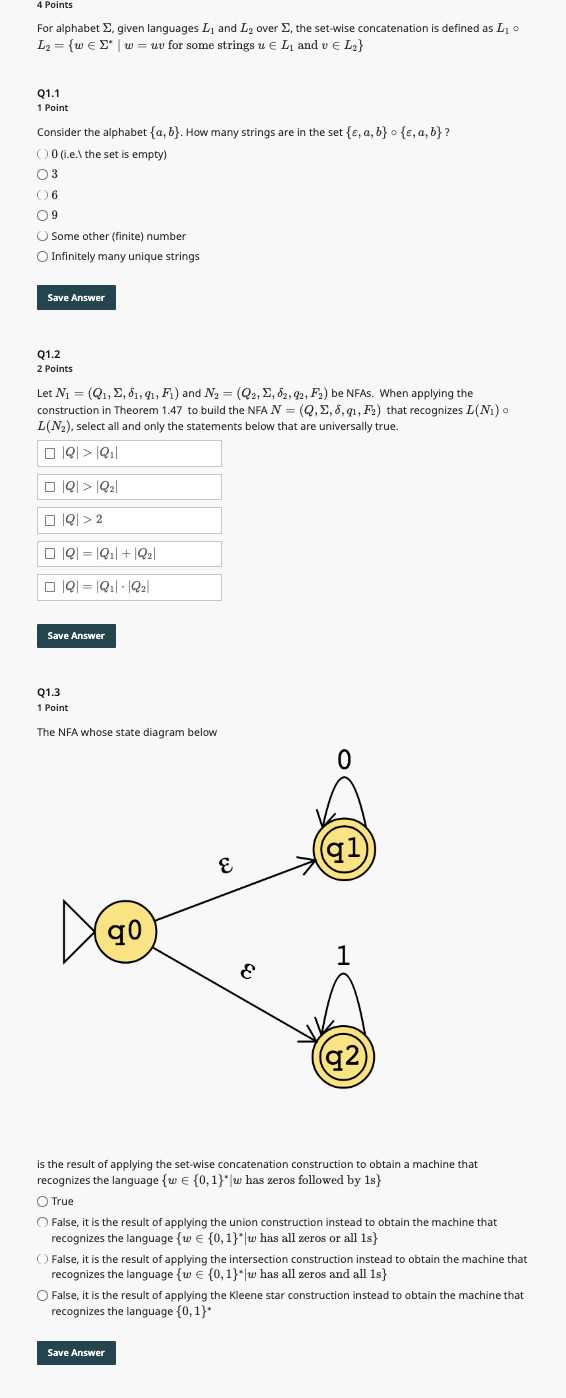
The NFA whose state diagram below

is the result of applying the set$-$wise concatenation construction to obtain a machine that

recognizes the language $\{\begin{array}{ccc}\text{w}\text{i}\text{n}& \{0,& 1{\}}^{**}|w\end{array}$ has zeros followed by $\{$:$1(s)\}$

True

False, it is the result of applying the union construction instead to obtain the machine that

recognizes the language $\{\begin{array}{ccc}\text{w}\text{i}\text{n}& \{0,& 1{\}}^{**}|w\end{array}$ has all zeros or all $\{$:$1(s)\}$

$()$ False, it is the result of applying the intersection construction instead to obtain the machine that

recognizes the language $\{\begin{array}{ccc}\text{w}\text{i}\text{n}& \{0,& 1{\}}^{**}|w\end{array}$ has all zeros and all $\{$:$1(s)\}$

False, it is the result of applying the Kleene star construction instead to obtain the machine that

recognizes the language $\{0,1{\}}^{**}$