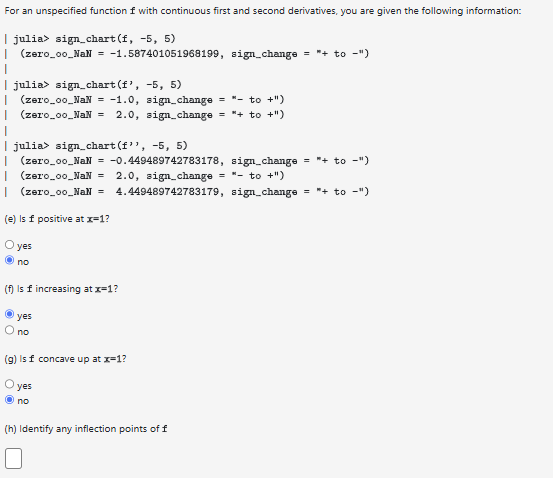
Question: For an unspecified function ( mathbf { f } ) with continuous first and second derivatives, you are given the following information:
For an unspecified function mathbff with continuous first and second derivatives, you are given the following information:
julia signchartf
zeroooNall signchange to
julia signchartf
zeroooNaN signchange to
zeroNaN signchange to
julia signchartf
zeroooNall signchange to
zerooNaN signchange to
zeroooNall signchange to
e Is f positive at mathrmxyesno
f Is f increasing at xyesno
g Is f concave up at xyesno
h Identify any inflection points of mathbff
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


