for any >0

(1)

define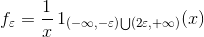

proof When 0, f has a limit in the meaning of the distribution (D(R)) and calculate the limit.

(2)

define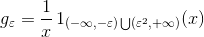

proof When 0, g has no limit in the definition of distribution

(3) define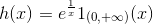

proof There is no u D(R), so that for any D((0, )),

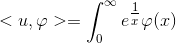
(u: D()C

)

1((a,b))(x)=1 (x in (a,b))

fe=-11-20,-)U(26, +00) (2) T 9 = 11-00,--)U(C2, +00) (2) T h() = e. 10,+) (2) = 1 (x) Given 2 CR, consider the Frechet space C(12) with the family of seminorms Pn(f) = sup]D f(x), n > 0, al 0. Given a compact subset K of 12, define DK = {fe C(12) : support(f) C K}. With the topology induced by C(12), DK is a Frechet space. Observe that in this space the topology is also induced by the seminorms || | ||n = sup D f(x)], n > 0. al= 1 (x) Given 2 CR, consider the Frechet space C(12) with the family of seminorms Pn(f) = sup]D f(x), n > 0, al 0. Given a compact subset K of 12, define DK = {fe C(12) : support(f) C K}. With the topology induced by C(12), DK is a Frechet space. Observe that in this space the topology is also induced by the seminorms || | ||n = sup D f(x)], n > 0. al