Question: For any real number c, define as an integer d such that ?z with 0 ? z always existswe will simply take that as an

For any real number c, define 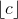as an integer d such that ?z with 0 ? z always existswe will simply take that as an axiom.

(a) (15 points) Prove that for any c, 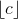?z with 0 ? z always existswe will simply take that as is unique

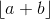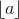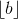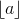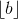(b) (20 points) Prove that for any a, b, an axiom. (a) (15 points) Prove that for any c, is unique is equal to + + or + + 1. or image text in transcribed + + 1.

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Databases Questions!

chapter 5 INTRODUCTION TO MATRIX ALGEBRA GOALS The purpose of this chapter is to introduce you to matrix algebra, which has many applications. You are already familiar with several algebras:...

1) Find all real solutions of: 4 2 2 x + x =3 2 x 4 + x23=0 4 2 2 2 x 2 x +3 x 3=0 x ( 21)=0 2 x 2 ( x 21)+ 3 ( 2 x2 +3 ) ( x 21 ) =0 ( 2 x2 +3 ) =0 2 2 x =3 3 x 2= 2 3 x= 2 3 x= i 2 2) Given the...

3 ,,uoh "gram 3 Eww 3 m T mm H a 3 .2 ' m w .,.m.av>v 3. m. @3on we geonwoaoa mm H "with M'nr H E. wads + we A at. ES 0 3.8V WEE 3563 mo wow 23 E m \"9H .3 avgmeMm\" mnemagouom Aggy\"...

\fCOMPLEX VARIABLES AND APPLICATIONS Eighth Edition James Ward Brown Professor of Mathematics The University of Michigan-Dearborn Ruel V. Churchill Late Professor of Mathematics The University of...

Transporting Efficiency Query You will a query to calculate the number of days between the date an order was placed and the date the order was shipped for each order. The result of your work will be...

Math\t107-6381\t-\tQuiz\t#4\t-\tSchultz\t-\tDue\tFebruary\t21,\t2016\t-\tpage\t1\tof 3 Follow\tthese\tdirections\tcarefully. This\tquiz\tis\tdue\tby\t11:59\tEastern\ttime\ton\tFebruary\t21,\t2016. o...

E Test: Chapter 5 Test Question list 0 Question 1 0 Question 2 0 Question 3 0 Question 4 0 Question 5 0 Question 6 0 Question 7 0 Question 8 I? Find the anlidelivative utthe given derivative do (X +...

This question involves the use of AGGREGATE linear PYTHOIN regression on the Auto data set. (a) Perform a simple linear regression with mpg as the response and horsepower as the predictor. Describe...

Briefly describe ASCII and Unicode and draw attention to any relationship between them. [3 marks] (b) Briefly explain what a Reader is in the context of reading characters from data. [3 marks] A...

Selected accounting data as at December 31, 2019 for Huma Delivery follows: Cash Accounts payable Accounts receivable Salary payable Supplies Unearned revenue Prepaid rent Mortgage payable (due 2023)...

Japanese industry is often praised for its just-in-time inventory practice between industrial buyers and industrial sellers. In the context of the Days Receivables turnover in Exhibit 19.5, what is...

Finance companies are the most dominant lenders of credit to households in the United States with commercial banks ranked second as consumer lenders. True False

4 parts Kessel Company purchased a building and land with a fair market value of $475,000 (building, $300 000 and land, $175.000) on January 1, 2024 Kessel signed a 25-year, 8% mortgage payatle....

3. Explain to a manager how to ensure that transfer of training occurs.

4. Discuss the implications of identical elements, stimulus generalization, and cognitive theories for transfer of training.

2. Create a work environment that will facilitate transfer of training.