Question: Consider k = 2 and m = 1. Let X1,..., XnMulti3(1,0), where 0 03. For simplicity, denote X = (X1,..., Xik) and Xio =

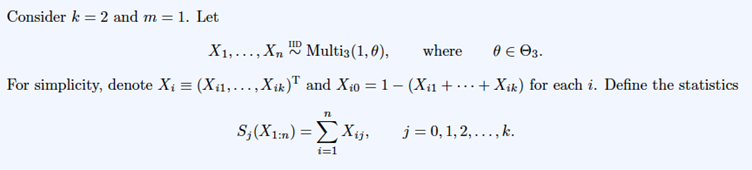
Consider k = 2 and m= 1. LetX1, ..., XnMultis(1,6),where?3.For simplicity, denote Xi = (Xi1, ..., Xik) and X 10 =1- (Xi 2. Prove that T(X1:n) = (S1(X1:n), S2(X1:n)) is a sufficient statistic (SS) for 6 by using(a) (15%) the definition of suffi

Consider k = 2 and m = 1. Let X1,..., XnMulti3(1,0), where 0 03. For simplicity, denote X = (X1,..., Xik) and Xio = 1 - (Xi1 + + Xik) for each i. Define the statistics 12 S; (X1:n) = Xij, i=1 j= 0, 1, 2,..., k. 2. Prove that T(X1:n) = (S1(X1:n), S2(X1:n)) is a sufficient statistic (SS) for by using (a) (15%) the definition of sufficiency; (b) (10%) Neyman-Fisher factorization theorem; and (c) (15%) the properties of exponential family.

Step by Step Solution

★★★★★

3.46 Rating (146 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

a Let TX1n S1X1n S2X1n be the proposed statistic We want to show that for any the conditi... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Accounting Questions!

For = 0.2 s1, produce computer plots like those shown in Figure 3-15 for a sinusoidal driven, damped oscillator where xp(t), xc(t), and the sum x(t) are shown . Let k = 1kg/s2 and m = 1kg. Do this...

For each of the following errors, considered individually, indicate whether the error would cause the trial balance totals to be unequal. If the error would cause the trial balance totals to be...

Education: Exam Scores Professor Gill has taught general psychology for many years. During the semester, she gives three multiple-choice exams, each worth 100 points. At the end of the course, Dr....

1. A player throws a fair die and simultaneously flips a fair coin. If the coin lands heads, then she wins twice, and if tails, then one-half of the value that appears on the die. Determine her...

(i) Let X have binomial distribution b(p, n), and consider testing H : p = p0 at level against the alternatives K : p/q 1 2 p0/q0 or 2p0/q0. For = .05 determine the smallest sample size for which...

Consider Hoare triples of the form {T} V := E {V = E} where T is the atomic formula 'true' and V and E range over variables and expressions, respectively. (i) Write down an instance of such a triple...

9. (Continued from HW11, #9) Let X1, . . . , Xn iid Beta(, 1). (a) Using 2T as a pivot, find the 100(1 )% confidence interval for . (b) Invert this confidence interval to find a rejection region of...

Consider the following problem. Minimize Z = 5x1 + c2x2, Subject to and x1 ¥ 0, x2 ¥ 0, where x1 represents the level of activity 1 and x2 represents the level of activity 2. The values of...

tables are made of wood wood cost is $100 for table tables are made by worker, ho paid to the morken per table workers assembling tables are supervised by a factory supervisor who is paid $5000 per...

Ami stops to fill her car with gas at Local Gas Station. Unbeknownst to Ami, Amari, one of the employees at the store, has placed a device on the pump that allows her to steal the credit card number....

Design a custom date function that showcases your coding abilities and originality. The function should take 3 inputs: the output of the Get-Date cmdlet, and two additional parameters. It must...

5. Find the tension in the cable and the force exerted by the hinge on the beam. The beam has mass 50.0 kg and length 7.00m. (754N; 492N at 10.2 below hzntl) 80.0 30.0 7.00 m 2.00 m

The ethical principle of applies to the security of payroll records. Multiple Choice Professional Competence and Due Care Integrity Confidentiality Objectivity and Independence

QS 1-7 (Algo) Applying the accounting equation LO A1 a. Total assets of Charter Company equal $730,000 and its equity is $435,000. What is the amount of its liabilities? b. Total assets of Martin...

A statistical program is recommended. Consider the following data for two variables, x and y x 22 24 26 30 35 40 v 12 | 22 | 32 | 36 (a) Develop an estimated regression equation for the data of the...

What kind of financial pressures can an LBO cause?

If for n = 1, 2,..., the r.v.s {Xn} and {Yn} are uniformly integrable, show that {Xn + Yn} are also uniformly integrable?

Carry out the details of the proof of the Corollary to Theorem 14.

Let A1, A2,... be arbitrary events in ((, A), and define Bm by: Bm = "Am is the first event which occurs among the events A1, A2,...," m ¥ 1. Then (i) Express Bm in terms of Ans, m ¥ 1. (ii)...

Bruno SpA has decided to expand its operations. The bookkeeper recently completed the following statement of financial position in order to obtain additional funds for expansion. Instructions Prepare...

The statement of financial position of Kishwaukee Ltd. as of December 31, 2019, is as follows. Note 1: Goodwill in the amount of 120,000 was recognized because the company believed that book value...

The adjusted trial balance of Asian-Pacific Ltd. and other related information for the year 2019 are presented below (amounts in thousands). Additional information: 1. The average-cost method of...