For each function f(n) and time t in the following table, determine the largest size n of a problem that can be solved in time t assuming that the algorithm to solve the problem takes f(n) microseconds. Recall that log n denotes the logarithm in base 2 of n.

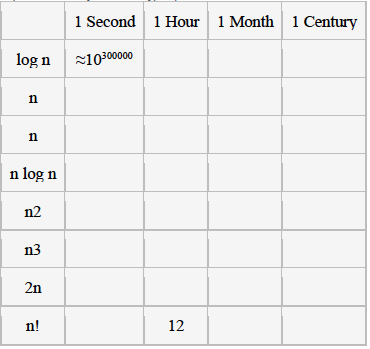
Please show your work for each function, so I can better understand how to work these problems out.

\begin{tabular}{|c|c|c|c|c|} \hline & 1 Second & 1 Hour & 1 Month & 1 Century \\ \hline logn & 10300000 & & & \\ \hline n & & & & \\ \hline n & & & & \\ \hline nlogn & & & & \\ \hline n2 & & & & \\ \hline n3 & & & & \\ \hline 2n & & & & \\ \hline n! & & 12 & & \\ \hline \end{tabular}