Question: For each vector field F(x, y, z), compute the curl of F and, if possible, find a function f(x, y, z) so that F=Vf.

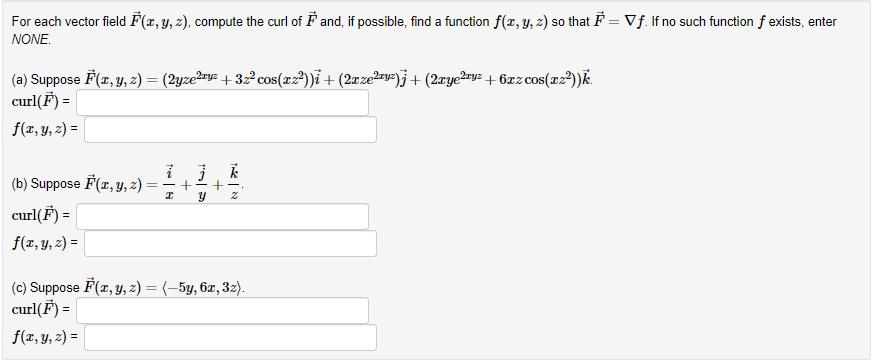
For each vector field F(x, y, z), compute the curl of F

For each vector field F(x, y, z), compute the curl of F and, if possible, find a function f(x, y, z) so that F=Vf. If no such function f exists, enter NONE. (a) Suppose F(x, y, z) = (2yzeyz + 32 cos(xz))i + (2xze)j + (2ryeyz + 6xz cos(xz))k. curl(F) = f(x, y, z) = (b) Suppose F(x, y, z) curl(F) = f(x, y, z) = the H i == + 3 19 +-. Z (c) Suppose F(x, y, z) = (-5y,6x, 32). curl(F) = f(x, y, z) =

Step by Step Solution

★★★★★

3.32 Rating (155 Votes )

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

The following additional information is available for the Dr. Ivan and Irene Incisor family from Chapters 1-5. Ivan's grandfather died and left a portfolio of municipal bonds. In 2012, they pay Ivan...

find one example from the news media that you can link --either videos, podcasts, articles, reports, television broadcasts, etc.--that exhibit what you take to be a valid and sound deductive argument.

The following additional information is available for the Dr. Ivan and Irene Incisor family. The Incisors own a rental beach house in Hawaii. The beach house was rented for the full year during 2012...

a. Give an example of a vector field F (x, y, z) that has value 0 at only one point and such that curl F is nonzero everywhere. Be sure to identify the point and compute the curl. b. Give an example...

QUESTION 3 (20 MARKS) (a) The velocity of an object at time t is given by v(t) = (t + 2) i + tsinh taj + et/3k, and the initial position of the object is r(0) = 6k. Find the position vector r(t) of...

Consider the radial vector field F = (x, y, z). Let D be the solid between the paraboloids (a) Let C be the intersection curve of the two paraboloids, oriented counterclockwise. Find a...

Costs associated with the manufacture of miniature high-sensitivity piezoresistive pressure transducers is $81,000 per year. A clever industrial engineer found that by spending $17,000 now to...

12 (1 point) Consider the vector field F (x, y, z) = (2z + 4y) i + (2z + 4x) j + (2y + 2x) k. a) Find a function f such that F - Vf and f(0, 0, 0) = 0. f (z, y, z) = b) Suppose C is any curve from...

QUESTION 6 Converting from rectangular Coordinate to Spherical Coordinate Choose one . 4 points Change p = (1, 1, 0) from rectangular to spherical coordinates. O P = (r, 0, $) = (2, 7' 7) O p = (r,...

s 1. Find the center of mass of the following plane region with variable density. Describe the distribution of mass in the region: The upper half (y 0) of the y 2 2 disk bounded by the circle x + y...

Massachusetts Casualty Insurance Company decides to enter the leasing business. It acquires a specialized packaging machine for $300,000 cash and leases it for a period of six years, after which the...

Prepare a variance (horizontal) analysis for the three most current years for each of the financial statements listed below. Provide an explanation for significant variances in the financial...

Fill in the Blank Question Fill in the blank question. Less coordinated decision making by executives and supervisors is a worker productivity factor that leads to of scale

If .] denotes greatest integer function and f (a) = (cos [7] # + cos [-n] #) t %3D the value of f(] ) +f ([-2] ) = (A) + 1 V2 (B) 1- (C) -1 (D) none of these

The period of f (x) = (sgn ||) + (sin ) + (cot a (A) T/2 (B) T (C) 27 (D) not defined

If 3 (+)V e R, 1 Va ER,T 4" f (2) = 2" 4 12 the value of f (log; 2) + f (log(1/3) (2/3) = (A) 1 (B) 2 (C) 4 (D) 6

Suppose f(x,y)=x2+y28x6y+5 (A) How many critical points does f have iR2? (B) If there is a local minimum, what is the value of the discriminant D at that point? If there is none, type N. (C) If there...

Determine the total pressure on a circular plate of diameter 1.5 m which is placed vertically in water in such a way that the center of plate is 3m below the free surface of water. Find the position...

Frequent flier miles would be an example of which barrier to entry?Multiple Choicebuilding customer loyaltiessecuring access to supply of key resourcescreating product uniquenesshuilding in switehing...

If f(x) = x2 - 1 and g(x) = 2/x, find formulas for the following and state their domains. (a) (f g) (x) (b) f4(x) + g4 (x) (c) (f g) (x) (d) (g f) (x)

Let F = 2i + xzj + z3 k and S be the boundary of the surface z = xy2, 0 ( x ( 1, 0 ( y 1, oriented counter clock wise as viewed from above. Evaluate F.T ds.

Find examples to show that if lim f(x)g(x) lim f(x or lim g[:x

Under what circumstances will this change?

What are the behaviours that show this character is dealing with a conflict using Submission? (Remember that the intensity increases as the character moves from 1st option to 2nd option to 3rd...

What other characters in the story have an opposite sequence of