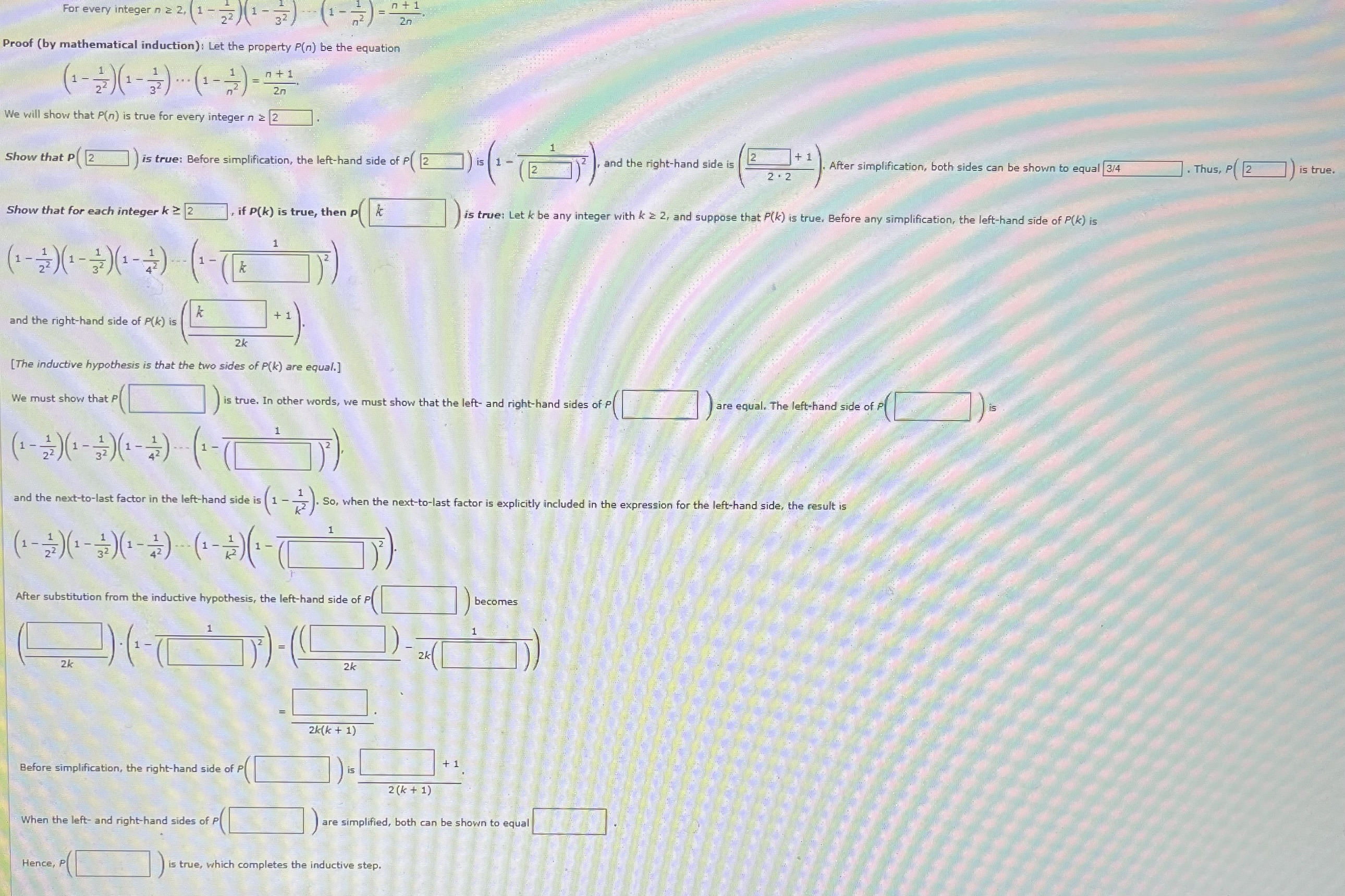
For every integer n 2 2. (1 22 1 - 32 1 72 - n+1 27 Proof (by mathematical induction): Let the property P(n) be the equation (1 - 2 ) (1 -) ... ( 1-#) n + 1 We will show that P(n) is true for every integer n 2 2 Show that P [2 )is true: Before simplification, the left-hand side of P 2 1 - and the right-hand side is 2 2 . After simplification, both sides can be shown to equal 3/4 2- 2 . Thus, P [2 is true. Show that for each integer k 2 2 , if P(k) is true, then p k is true: Let k be any integer with k 2 2, and suppose that P(k) is true. Before any simplification, the left-hand side of P(k) is and the right-hand side of P(k) is + 1 2k [The inductive hypothesis is that the two sides of P(k) are equal.] We must show that P is true. In other words, we must show that the left- and right-hand sides of P are equal. The left-hand side of P (1-2 ) (1-37)(1-#)(1-7 and the next-to-last factor in the left-hand side is (1 - -2 ). So, when the next-to-last factor is explicitly included in the expression for the left-hand side, the result Is ( 2 - 2 ) ( 2 - 3 ) ( 1 - # ) (1-# )(1- After substitution from the inductive hypothesis, the left-hand side of P becomes 2 k 2k 2k 2k(k + 1) Before simplification, the right-hand side of P 2 (k + 1) When the left- and right-hand sides of P are simplified, both can be shown to equal Hence, P is true, which completes the inductive step