Question: For F 1 ( x , y ) = 1 4 x 4 + x 2 y + y 2 and F 2 ( x
For and find the second derivative matrices and :
is positive definite, so is concave up convex Find the minimum point of and the saddle point of look where first derivatives are zero
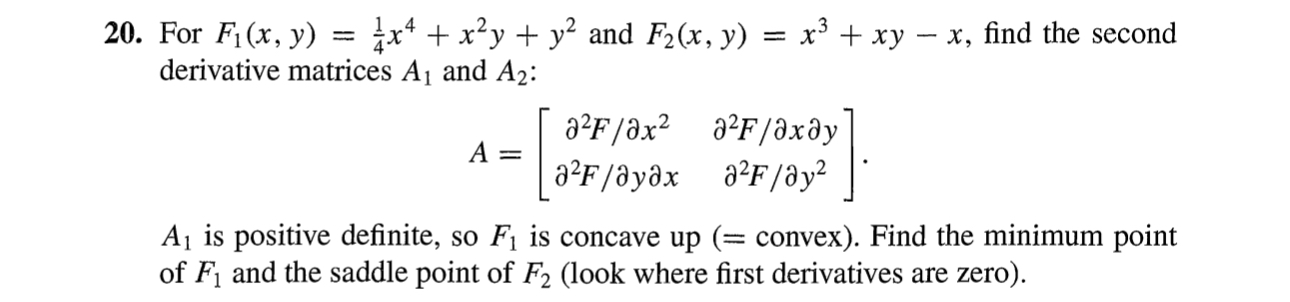
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


