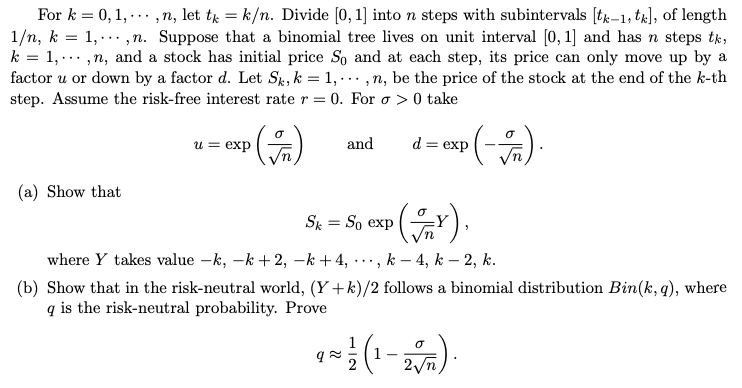
For k = 0,1,..., n, let tk = k. Divide (0, 1) into n steps with subintervals (tk-1, tk], of length 1, k = 1,...,n. Suppose that a binomial tree lives on unit interval [0, 1] and has n steps tk, k = 1,...,n, and a stock has initial price So and at each step, its price can only move up by a factor u or down by a factor d. Let Sk, k = 1,...,n, be the price of the stock at the end of the k-th step. Assume the risk-free interest rate r = 0. For o >0 take u= exp () and d= exp ( - ). (a) Show that Sk= So exp (my), where Y takes value -k, -k +2, -k +4, ..., k-4, k-2, k. (b) Show that in the risk-neutral world, (Y+k)/2 follows a binomial distribution Bin(k, ), where q is the risk-neutral probability. Prove q=}(1-2) For k = 0,1,..., n, let tk = k. Divide (0, 1) into n steps with subintervals (tk-1, tk], of length 1, k = 1,...,n. Suppose that a binomial tree lives on unit interval [0, 1] and has n steps tk, k = 1,...,n, and a stock has initial price So and at each step, its price can only move up by a factor u or down by a factor d. Let Sk, k = 1,...,n, be the price of the stock at the end of the k-th step. Assume the risk-free interest rate r = 0. For o >0 take u= exp () and d= exp ( - ). (a) Show that Sk= So exp (my), where Y takes value -k, -k +2, -k +4, ..., k-4, k-2, k. (b) Show that in the risk-neutral world, (Y+k)/2 follows a binomial distribution Bin(k, ), where q is the risk-neutral probability. Prove q=}(1-2)