For MATLAB programming: Put all answers in a MATLAB script named file6.m. Include the following files: file6.m and testpi.m. Make sure that figure 1 is plotted when script is executed. Use double precision unless otherwise stated. Problem 1: Use nested for loops to perform the following exercises. Do not use function mean. (a) Create the 3-D function: M(x, y, z) = 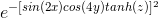in a rectangular domain with x = [-2:0.01:2]; y = [-1:0.01:1] and z = [0:0.01:1]. Matrix M should have the dimension of length(x) by length(y) by length(z). Set p1a=M. (b) Compute the average value of M over the entire rectangular domain and put the answer into p1b. The answer should be a single number. (c) Compute the average values of M over the x-y planes and put the answer into p1c. The answer should be a vector with the dimension of length(z). (d) Compute the average values of M along the z-direction and put the answer into p1d. The answer should be a 2-D matrix with the dimension of length(x) by length(y). (e) Create figure 1. Use function surf to plot the answer in part (d), e.g. p1d, versus x and y. Remember to label the axes and give the figure a title. Set p1e='See figure 1'. Problem 2: A ball is released from a 10 m high roof and bounces three quarters as high on each successive bounce. (a,b) After traveling a total of 69.99 m (up and down motion), how many times did the ball bounce? Put the answer in p2a. What is the height of the most recent bounce? Put the answer in p2b. (c,d) For the 32th bounce, how high did the ball go? Put the answer in p2c. How many meters did the ball travel (up and down motion) in total prior to the 32th bounce? Put the answer in p2d. Problem 3: Leibniz found that 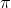can be approximated by the following series:

.

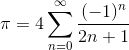Madhava (with Leibniz) later suggested an alternative series: .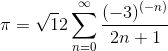 In this exercise, you are asked to write a function testpi.m to compare how fast the two series can approximate the value of 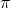for a given tolerance. The function should have the following declaration: function [api, nterm] = testpi(tol, method) where tol is the input tolerance defined as the difference between the approximated and the default value of in MATLAB divided by the default value. Method is a string input being either 'Leibniz' or 'Madhava'. The function outputs are the approximated value of 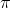api and the number of terms nterm in the series needed to compute the approximate value. In the function, you may want to consider the relationship between abs(api-pi)/pi and tol as a condition to truncate n in the two series above. Give the function a description. In the following exercises, set the tolerance to 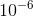. (a) Set p3a=evalc('help testpi'). (b,c) For the Leibniz series, what is the approximated value of 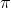and how many terms of the series are needed to compute that value? Put the answers in p3b and p3c, respectively. (d,e) For the Madhava series, what is the approximated value of 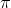and how many terms of the series are needed to compute that value? Put the answers in p3d and p3e, respectively. (f) Which method converges faster? Give answer in p3f = '... series converges faster'.