For part A,

This is an example of a function definition.

PLEASE DO NOT COPY AND PASTE AN ANSWER FROM ANOTHER QUESTION

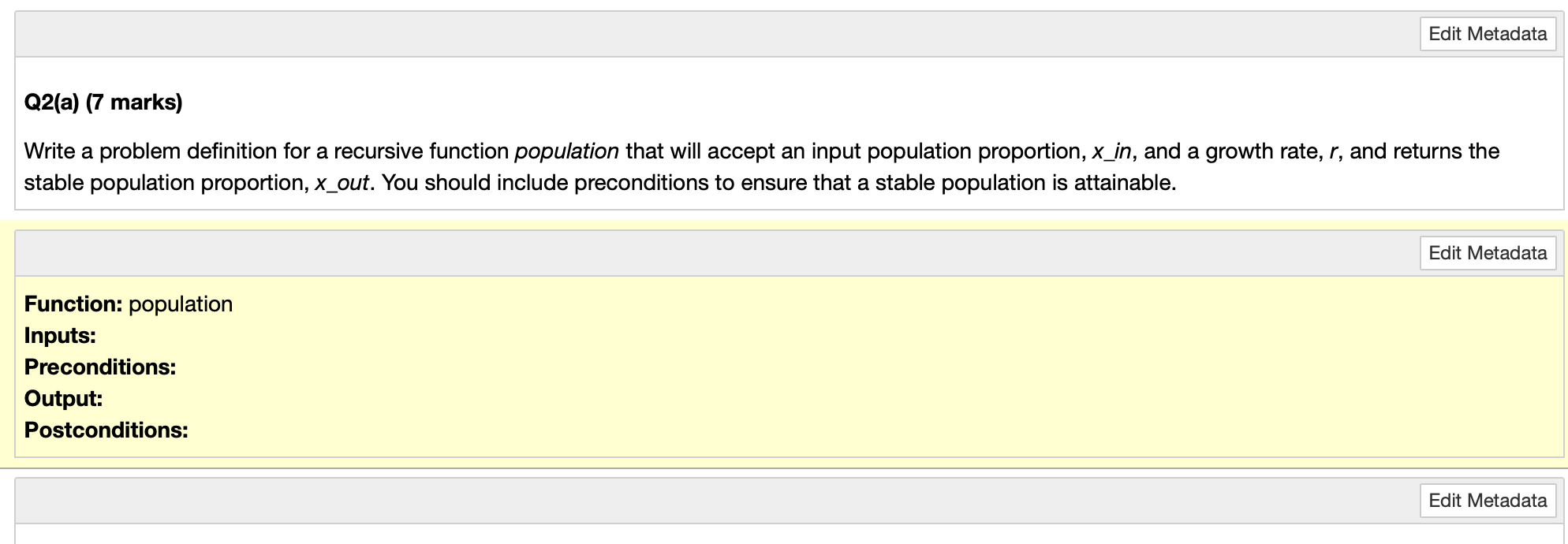
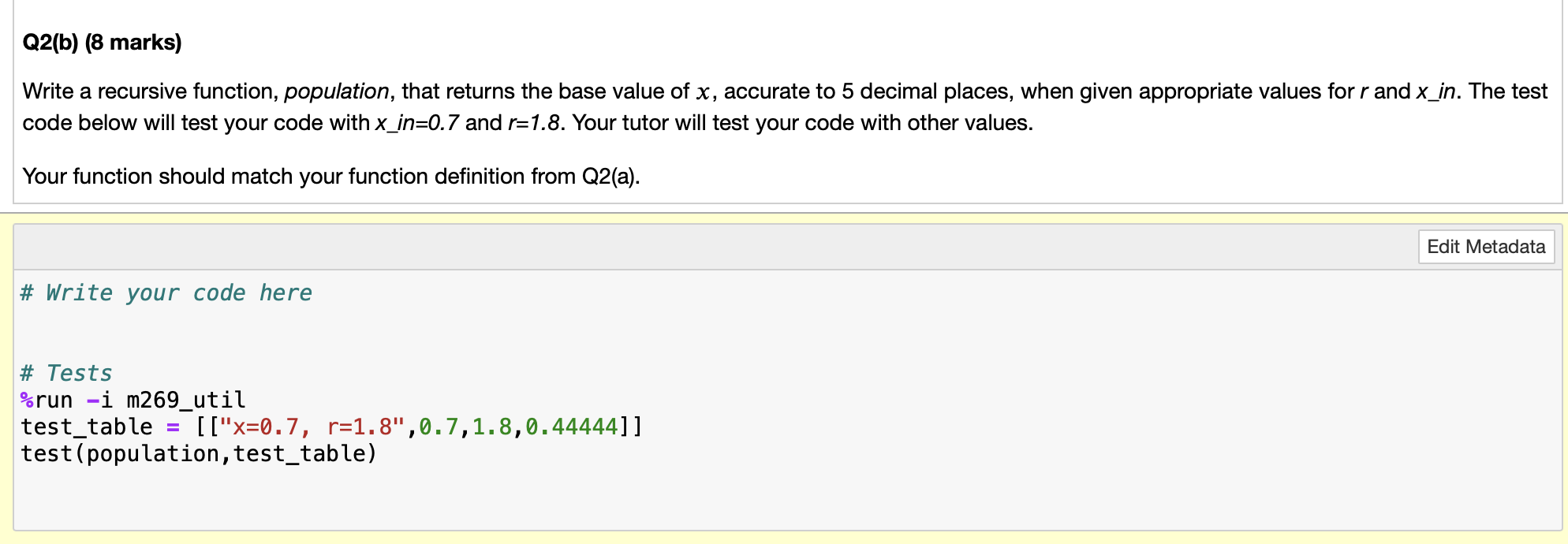
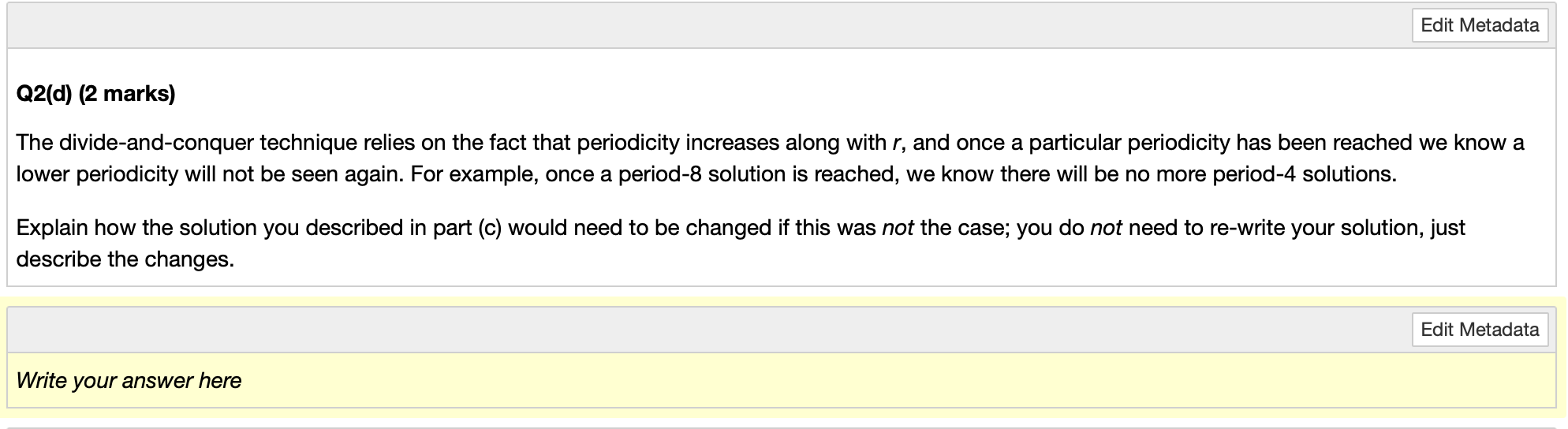
Function: double lettered Inputs: word, a string Preconditions: word contains only lowercase letters Output: is double lettered, a Boolean Postconditions: is double lettered is true if word contains two consecutive identical letters, else false - Think of the inputs and outputs as variable declarations - give each input and output a name and a type - The precondition is intended to say what conditions need to be true of the input data for it to be valid to call the function. Think of it a a logical expression and if the value is true it is valid to call the function. - The postcondition just says what the output will look like when the function is complete don't forget to handle any null or empty cases! Postconditions: priorities counts is a dictionary with keys representing priorities in the queue, and values representing frequencies of the priorities within the queue. An empty dictionary is returned if leather list is empty. The population growth of a particular animal can be modelled using the following recurrence relation: xn+1=rxn(1xn) The population is measured as a proportion of the maximum sustainable population, given the resources available. x represents the proportion, and n represents the year. For example, in year 0 if the maximum possible population was 1,000 and the current population was 500 , then x0 would be 0.5 . r represents the rate at which the population grows. There are two restrictions: - x0 must be between 0 and 1 (exclusive). - r must be greater than 1 . An example of the population growing over time could look like this, where the population at x0 is 0.7 of its maximum potential size, and r=1.8. All numbers are rounded to 5 decimal places. You can see from the table above that when rounded to 5 decimal places, x will reach a limiting value where xn=xn+1 and will remain stable. This will remain true as long as x0 is between 0 and 1 (exclusive), and r is between 1.0 and 3.1 (exclusive). Q2(a) (7 marks) Write a problem definition for a recursive function population that will accept an input population proportion, xin, and a growth rate, r, and returns the stable population proportion, xout. You should include preconditions to ensure that a stable population is attainable. Write a recursive function, population, that returns the base value of x, accurate to 5 decimal places, when given appropriate values for r and x in. The test code below will test your code with x_in=0.7 and r=1.8. Your tutor will test your code with other values. Your function should match your function definition from Q2(a). \# Write your code here \# Tests % run -i m269_util test_table =[[ "x=0.7, r=1.8,0.7,1.8,0.44444]] test(population, test_table) At the start of Question 2, we mentioned that r needs to be kept between 1.0 and 3.1 (exclusive) to maintain a stable population. When a period r of 3.1 is used, the population proportion converges to two alternating values. Using x=0.7 and r=3.1, for example, the resulting population proportions will alternate between 0.55802 and 0.76456 (your values may vary by 0.00001 depending on the method used). As the population alternates between two values, we call this a period-2 (21) solution. At higher values of r, we get a period-4 (22) solution (where the population converges to a sequence of four values repeated), then a period- 8(23) solution, and so on. This is known as the periodicity. When r reaches 3.7 , there is no periodic behaviour: it is described as chaotic. Outline in English how you could use a divide-and-conquer technique to identify the lowest value of r (to 4 decimal places) that leads to a periodicity of 2y where y is defined by the user. An outline in English should not be program code or pseudo-code; see Section 6.4 .1 for further guidance on outlining algorithms in English. Not using an English outline will lead to marks being deducted. You may assume that: - You have a function, calculate_periodicity ( ), which is passed a value r and returns the periodicity. - Solutions of increasing periods occur in increasing order as r increases between 3.1 and 3.7, so at some value of r the periodicity will stop returning 2n and will start returning 2n+1. At this point there will be no return to 2n. Your solution should return -1 if the given periodicity is not identified within the restrictions given. The divide-and-conquer technique relies on the fact that periodicity increases along with r, and once a particular periodicity has been reached we know a lower periodicity will not be seen again. For example, once a period-8 solution is reached, we know there will be no more period-4 solutions. Explain how the solution you described in part (c) would need to be changed if this was not the case; you do not need to re-write your solution, just describe the changes