For part a,b please fill the table provided. and for c you are required to make a new table

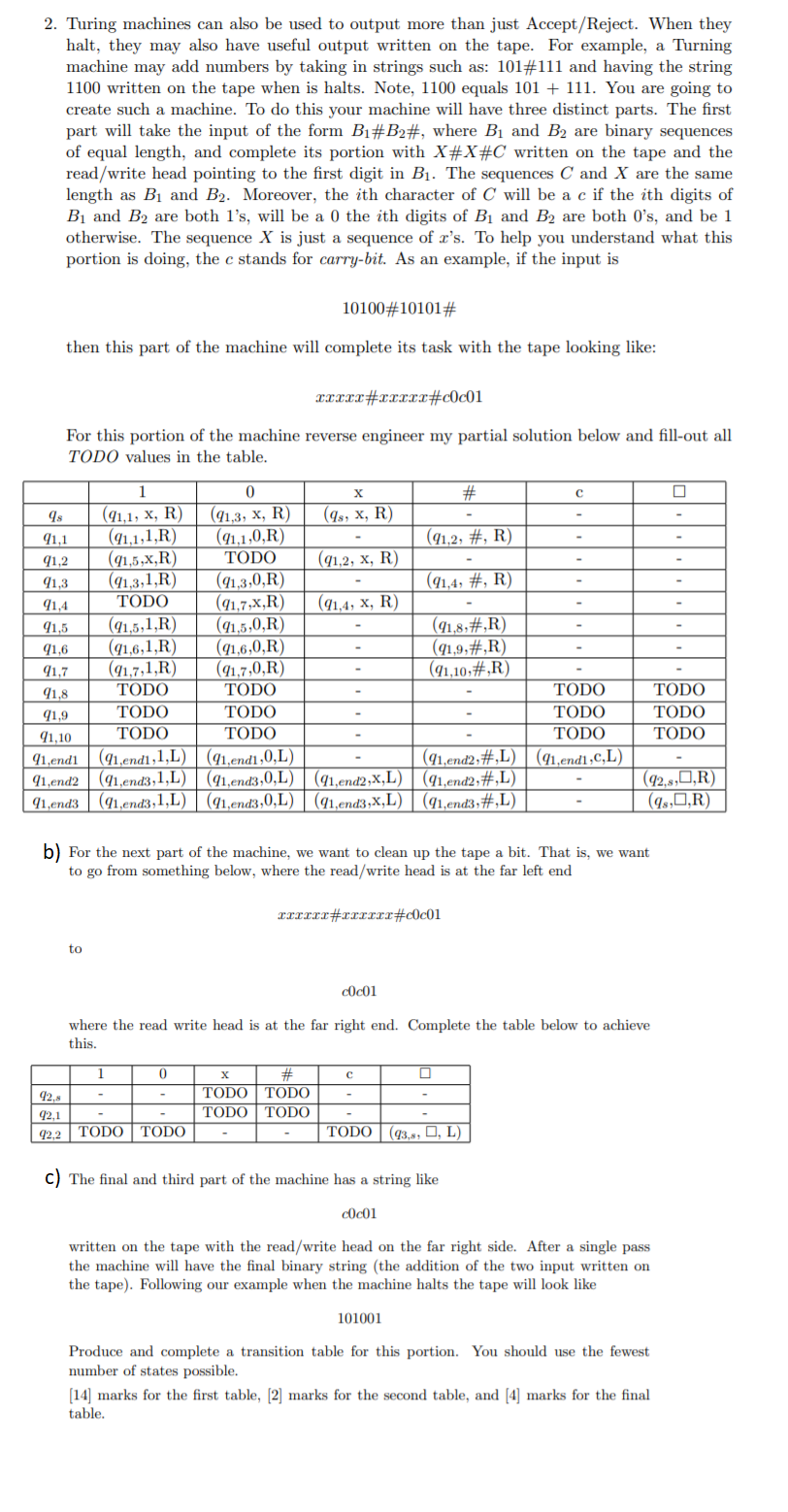
2. Turing machines can also be used to output more than just Accept/Reject. When they halt, they may also have useful output written on the tape. For example, a Turning machine may add numbers by taking in strings such as: 101#111 and having the string 1100 written on the tape when is halts. Note, 1100 equals 101 + 111. You are going to create such a machine. To do this your machine will have three distinct parts. The first part will take the input of the form B1#B2#, where Bi and B2 are binary sequences of equal length, and complete its portion with X X #C written on the tape and the read/write head pointing to the first digit in B1. The sequences C and X are the same length as B1 and B2. Moreover, the ith character of C will be a c if the ith digits of B1 and B2 are both l's, will be a 0 the ith digits of B1 and B2 are both O's, and be 1 otherwise. The sequence X is just a sequence of r's. To help you understand what this portion is doing, the c stands for carry-bit. As an example, if the input is 10100#10101# then this part of the machine will complete its task with the tape looking like: XIXxx#xxxxx#c0c01 For this portion of the machine reverse engineer my partial solution below and fill-out all TODO values in the table. # C D x (9s, x, R) - (912, X, R) 91,2, #, R) - - (91,4, #, R) 98 91,1 91,2 91, 3 91,4 91, 5 91, 6 91,7 91,8 91,9 91,10 91.endi 91,end2 91, end3 (91,4, x, R) 1 (91,1, x, R) (91,1,1,R) (91,5,x,R) 91,3,1,R) TODO 91,5,1,R) 9 1,6,1,R) 91.7,1, R T TODO TODO TODO (91.endi,1,L) 91,end3,1,L) (91,end3,1,L) 0 (91,3, X, R) (91,1,0,R) TODO (91,3,0,R) (91,7,x,R) (91,5,0,R) 91,6,0,R) (91.7,0,R) TODO TODO (91,8,#,R) (91,9,#,R) (91.10,#,R) TODO TODO TODO TODO TODO TODO (91, end1.c,L) - - (91.end1,0,L) (91,end3,0,L) (91.end3,0,L) - (91, end2,x,L) (91.end3,x,L) (91,end2, #,L) (91, end2,#,L) (91, end3,#,L 92,5,O,R) (9g,O,R) b) For the next part of the machine, we want to clean up the tape a bit. That is, we want to go from something below, where the read/write head is at the far left end Irrrrrrrrrrr#c0c01 c0c01 where the read write head is at the far right end. Complete the table below to achieve this. 1 0 C 0 42.5 x # TODO TODO TODO TODO 42,1 42.2 - T - TODO TODO TODO 93,5, 0, L) C) The final and third part of the machine has a string like c0c01 written on the tape with the read/write head on the far right side. After a single pass the machine will have the final binary string (the addition of the two input written on the tape). Following our example when the machine halts the tape will look like 101001 Produce and complete a transition table for this portion. You should use the fewest number of states possible. (14) marks for the first table, 2 marks for the second table, and (4) marks for the final table. 2. Turing machines can also be used to output more than just Accept/Reject. When they halt, they may also have useful output written on the tape. For example, a Turning machine may add numbers by taking in strings such as: 101#111 and having the string 1100 written on the tape when is halts. Note, 1100 equals 101 + 111. You are going to create such a machine. To do this your machine will have three distinct parts. The first part will take the input of the form B1#B2#, where Bi and B2 are binary sequences of equal length, and complete its portion with X X #C written on the tape and the read/write head pointing to the first digit in B1. The sequences C and X are the same length as B1 and B2. Moreover, the ith character of C will be a c if the ith digits of B1 and B2 are both l's, will be a 0 the ith digits of B1 and B2 are both O's, and be 1 otherwise. The sequence X is just a sequence of r's. To help you understand what this portion is doing, the c stands for carry-bit. As an example, if the input is 10100#10101# then this part of the machine will complete its task with the tape looking like: XIXxx#xxxxx#c0c01 For this portion of the machine reverse engineer my partial solution below and fill-out all TODO values in the table. # C D x (9s, x, R) - (912, X, R) 91,2, #, R) - - (91,4, #, R) 98 91,1 91,2 91, 3 91,4 91, 5 91, 6 91,7 91,8 91,9 91,10 91.endi 91,end2 91, end3 (91,4, x, R) 1 (91,1, x, R) (91,1,1,R) (91,5,x,R) 91,3,1,R) TODO 91,5,1,R) 9 1,6,1,R) 91.7,1, R T TODO TODO TODO (91.endi,1,L) 91,end3,1,L) (91,end3,1,L) 0 (91,3, X, R) (91,1,0,R) TODO (91,3,0,R) (91,7,x,R) (91,5,0,R) 91,6,0,R) (91.7,0,R) TODO TODO (91,8,#,R) (91,9,#,R) (91.10,#,R) TODO TODO TODO TODO TODO TODO (91, end1.c,L) - - (91.end1,0,L) (91,end3,0,L) (91.end3,0,L) - (91, end2,x,L) (91.end3,x,L) (91,end2, #,L) (91, end2,#,L) (91, end3,#,L 92,5,O,R) (9g,O,R) b) For the next part of the machine, we want to clean up the tape a bit. That is, we want to go from something below, where the read/write head is at the far left end Irrrrrrrrrrr#c0c01 c0c01 where the read write head is at the far right end. Complete the table below to achieve this. 1 0 C 0 42.5 x # TODO TODO TODO TODO 42,1 42.2 - T - TODO TODO TODO 93,5, 0, L) C) The final and third part of the machine has a string like c0c01 written on the tape with the read/write head on the far right side. After a single pass the machine will have the final binary string (the addition of the two input written on the tape). Following our example when the machine halts the tape will look like 101001 Produce and complete a transition table for this portion. You should use the fewest number of states possible. (14) marks for the first table, 2 marks for the second table, and (4) marks for the final table