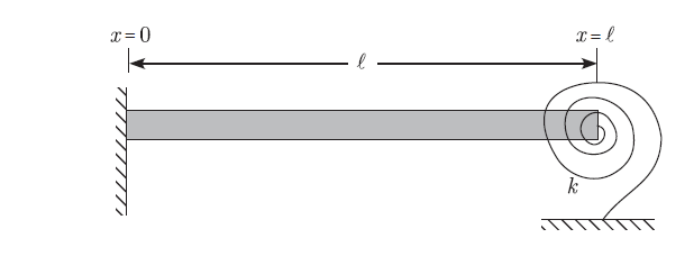
For the beam in the figure above, E $=69$E$9$ N$/$m$2,$ Density rho $=2698\mathrm{.}9$ kg$/$m$3,$ Length L $=20$ m$,$ Rectangular cross section with width, b $=1$ m and height, h $=0\mathrm{.}1$ m$,$ Torsional spring, k has a variable value. For instance, it may have a value, k $=200$ Nm$.($Note the units.$)$ The left end is cantilevered and the right end is constrained by the torsional spring. Remember that the torsional spring will restrict the rotation of the right end.

$($a$)$ Specify all the boundary conditions at the left end of the beam and the right end of the beam. The right end boundary conditions will be in terms of the spring constant, k$.$

$($b$)$ Specify the four equations that have to be solved to obtain the bending frequencies of the above beam.

$($c$)$ Obtain analytically the first bending frequencies of the beam in terms of k$.$

$($d$)$ Assume a non$-$dimensional parameter, $=$ and plot the value of the first bending frequency of the beam for the range: $=0$ through $=100.$

$($e$)$ What is the physical meaning of the system when $=0,$ and when $=$ infinity?

$($f$)$ Model the above beam in Nastran$/$Femap for $=0,10,50,$ and $100.$ Plot the first bending frequency values obtained from Nastran$/$Femap for these $$ values on top of the analytical solution from part $($d$).$