For the below example I am having difficulty understanding why when themv2 in the bottom equation is replaced by a substitution from the equation circled in red, but the sign is swapped from negative to positive.

Using the equation in red,mv2=?2mg(y2??y1?)

I'm guessing it's because of the direction of one of the forces but I'm failing to see the logic.

Thanks!!

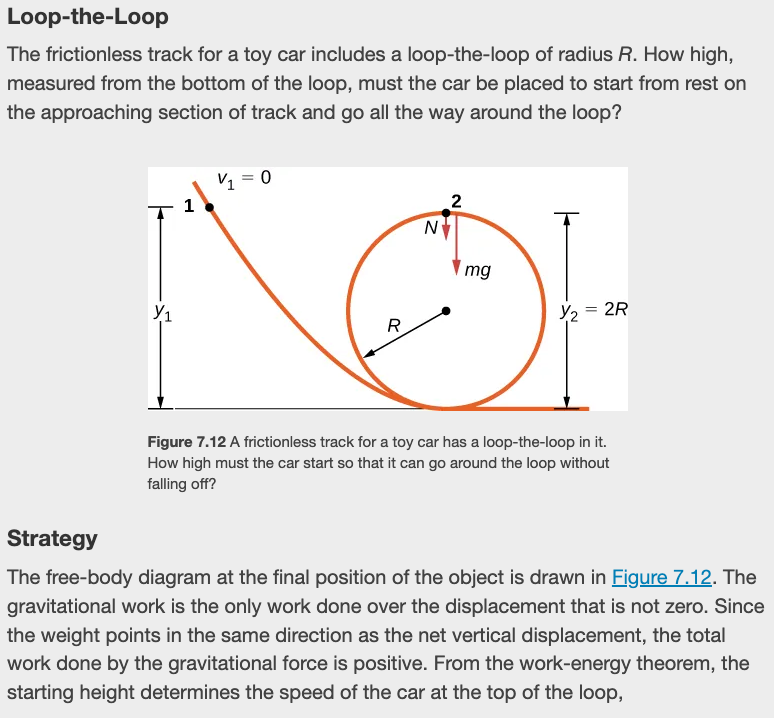
Loop-the-Loop The frictionless track for a toy car includes a loop-the-loop of radius R. How high, measured from the bottom of the loop, must the car be placed to start from rest on the approaching section of track and go all the way around the loop? V1 = 0 1 1mg y1 Y2 = 2R Figure 7.12 A frictionless track for a toy car has a loop-the-loop in it. How high must the car start so that it can go around the loop without falling off? Strategy The free-body diagram at the final position of the object is drawn in Figure 7.12. The gravitational work is the only work done over the displacement that is not zero. Since the weight points in the same direction as the net vertical displacement, the total work done by the gravitational force is positive. From the work-energy theorem, the starting height determines the speed of the car at the top of the loop,1 mg(y2 - y1) = -muzz where the notation is shown in the accompanying figure. At the top of the loop, the normal force and gravity are both down and the acceleration is centripetal, so F N + mg atop = = m m R The condition for maintaining contact with the track is that there must be some normal force, however slight; that is, N > 0. Substituting for u; and /, we can find the condition for y1 . Solution Implement the steps in the strategy to arrive at the desired result: mus -mgR(+ 2mg(y1 - 2R) 5R N = -mg + = > 0 or y1 > R R 2