For the case below, I tried calculating the Marginal Utility per hour to maximize the utility for the given time (10 hours). However, I'm not sure how to illustrate the budget constraint where there is no price. I would appreciate short explanations for a through d. Thank you!

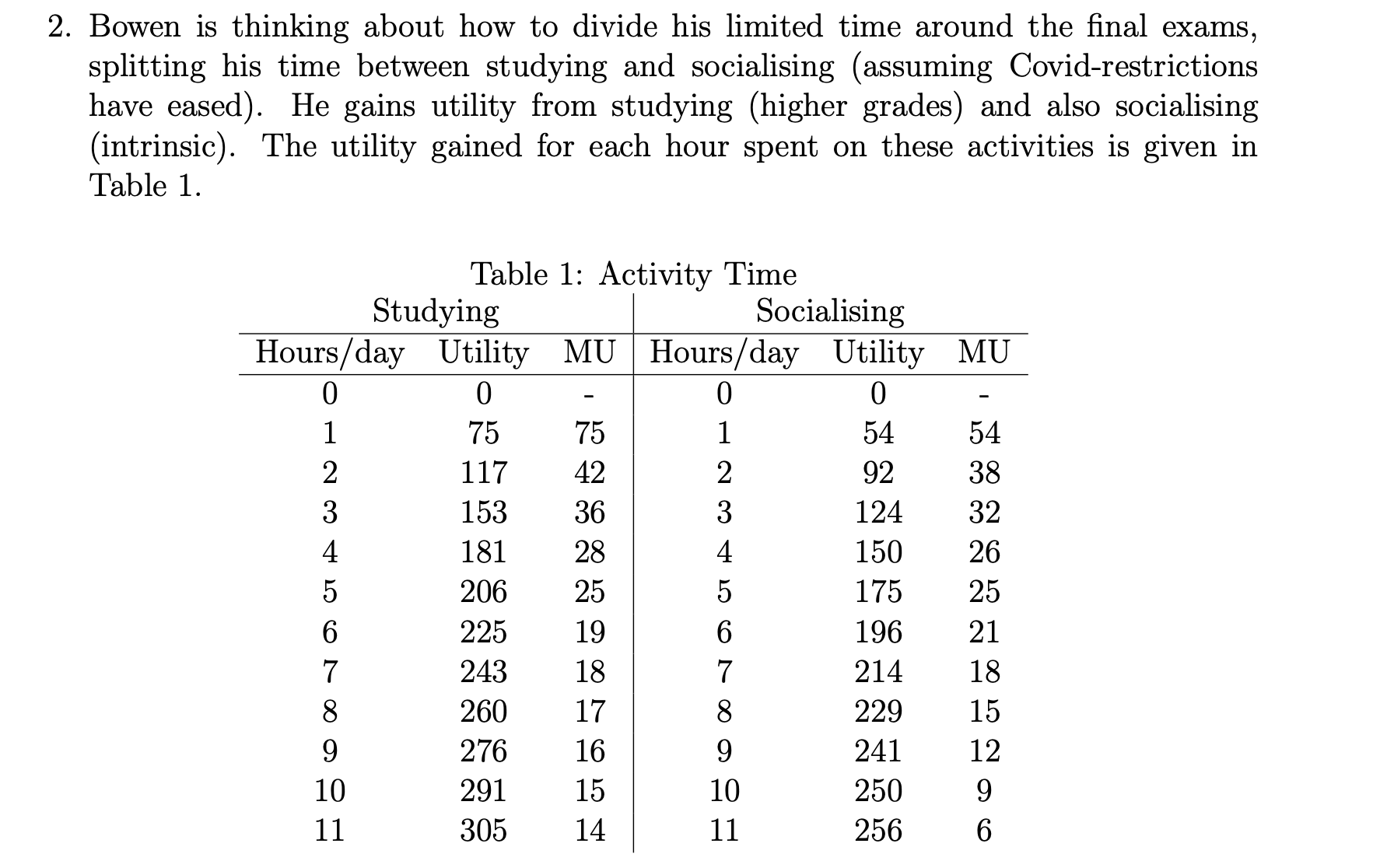
2. Bowen is thinking about how to divide his limited time around the nal exams, splitting his time between studying and socialising (assuming Covidrestrictions have eased). He gains utility from studying (higher grades) and also socialising (intrinsic). The utility gained for each hour spent on these activities is given in Table 1. Table 1: Activity Time Studying Socialising Hours / day Utility MU Hours / day Utility MU 0 0 0 0 1 75 75 1 54 54 2 117 42 2 92 38 3 153 36 3 124 32 4 181 28 4 150 26 5 206 25 5 175 25 6 225 19 6 196 21 7 243 18 7 214 18 8 260 17 8 229 15 9 276 16 9 241 12 10 291 15 10 250 9 11 305 14 11 256 6 a) Suppose Bowen has 10 hours each day to spend on activities to split between studying and socialising (where an hour spent socialising takes two hours of time, one socialising and one recovering). Show Bowen's budget constraint on an appropriate graph. b) How much time should Bowne spend studying and socialising each day? c) Explain the intuition as to why, at this activitybundle, Bowen's marginal utility per total hours spent is the same for both studying and socialising. d) As the exam time approaches, Bowen scales back all other activities (cook ing, cleaning, etc.) so now has 15 hours each day to spend on studying and socialising. How much time should he now spend on each activity