Question: For the purposes of this problem, we will define a generalized context - free grammar as a four - tuple ( G = (
For the purposes of this problem, we will define a "generalized contextfree grammar" as a fourtuple G N T P x where N is the set of nonterminal symbols, T is the set of terminal symbols, N cap T emptyset P subseteq N times N cup T is a finite set of production rules, and x in N cup T is the initial sentence form, known as the axiom. We define the derivation relation RightarrowG in grammar G in the same way as for contextfree grammars, and the language generated by grammar G is given as in phot. Clearly, every contextfree grammar is also a generalized contextfree grammar.
Determine whether for every generalized contextfree grammar G there exists a contextfree grammar G such that LG LG Prove your claim; in the case of constructing an equivalent grammar G prove its correctness using good mathematical inductiond
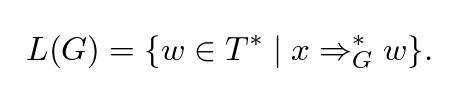
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


