For the sorting algorithm, we should use selection sort and insertion sort.

For the lecture slide mentioned in the first part, it was attached in the following part:

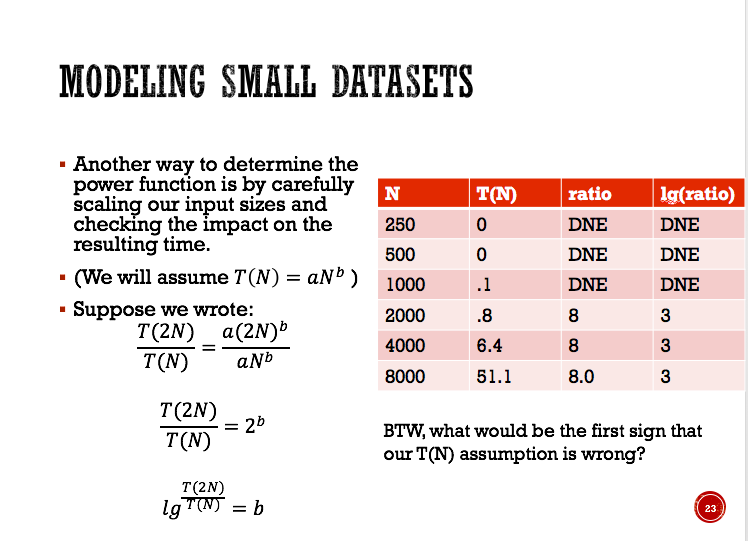
In addition, the source code mentioned in the second part was attached here:

Benchmarking Algorithms Summary: In this homework, you will be implementing code to generate test data and benchmark sorting. 1 Background In this assignmen you will practice predicting and verifying the impact of data "nature" on the run-time of sorting algorithms. As we have seen with algorithms like insertion sort, the runtime (even worse case like Big-Oh) can be ipacted by the nature of the input. To do this, we will create three different types of input data, that may give different results when sorted. Two sorting algorithms will then be benchmarked on these three types of data. Each algorithm will be run twice, for different dataset sizes, in order to get times that we can use to apply the doubling formula (See slide 23 (Modeling Small Datasets) in the Analysis of Algorithms slide deck for details on the doubling (2N) formula.) The doubling formula i g TENb. If we compute the formula, then we will be able to figure out the algorithm's Big-Oh for a particular type of input data, since they will be 0(n, b is simply the power. This document is separated into four sections: Background, Requirements, Testing, and Submission. You have almost finished reading the Background section already. In Requirements, we wil discuss what is expected of you in this homework. In Testing, we suggest some basic tests you use to start to verify your implementation. Lastly, Submission discusses how your source code should be submitted on BlackBoard. Benchmarking Algorithms Summary: In this homework, you will be implementing code to generate test data and benchmark sorting. 1 Background In this assignmen you will practice predicting and verifying the impact of data "nature" on the run-time of sorting algorithms. As we have seen with algorithms like insertion sort, the runtime (even worse case like Big-Oh) can be ipacted by the nature of the input. To do this, we will create three different types of input data, that may give different results when sorted. Two sorting algorithms will then be benchmarked on these three types of data. Each algorithm will be run twice, for different dataset sizes, in order to get times that we can use to apply the doubling formula (See slide 23 (Modeling Small Datasets) in the Analysis of Algorithms slide deck for details on the doubling (2N) formula.) The doubling formula i g TENb. If we compute the formula, then we will be able to figure out the algorithm's Big-Oh for a particular type of input data, since they will be 0(n, b is simply the power. This document is separated into four sections: Background, Requirements, Testing, and Submission. You have almost finished reading the Background section already. In Requirements, we wil discuss what is expected of you in this homework. In Testing, we suggest some basic tests you use to start to verify your implementation. Lastly, Submission discusses how your source code should be submitted on BlackBoard