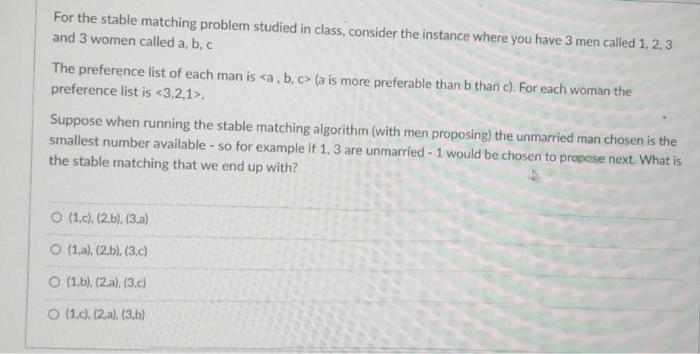
For the stable matching problem studied in class, consider the instance where you have 3 men called 1, 2,3 and 3 women called a,b,c The preference list of each man is ( a is more preferable than b than c). For each woman the preference list is 3,2,1. Suppose when running the stable matching algorithm (with men proposing) the unmarried man chosen is the smallest number available - so for example if 1,3 are unmarried - 1 would be chosen to propese next. What is the stable matching that we end up with? (1,c), (2,b),(3,a) (1,a), (2,b), (3,c) (1,b), (2,a), (3,c) (1,c), (2,a), (3,b)