Formulate a linear programming problem for the question

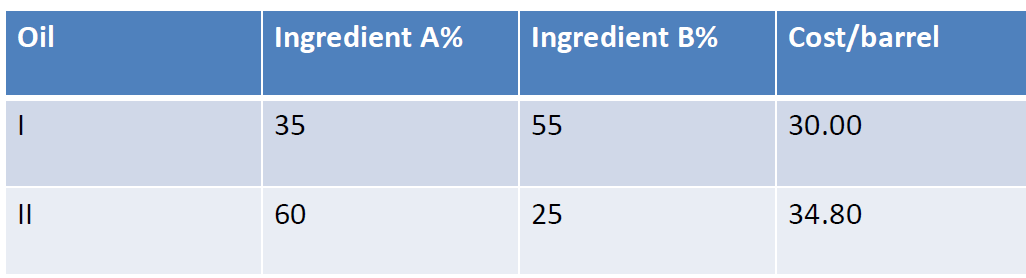
An oil company produces 2 grades of gasoline; R (regular) and E (economy) by mixing oils I and II. The table provides information regarding the oils. Note that all barrels contain 200 litres.

Answer the following questions separately to formulate a linear programming problem. At no instance should you go back to previous questions (except for the costs given in 1 ). Use only the current provided information and what is given at each question.

1) Given that a barrel of R sells for R100 and a barrel E sells for R150, write out the objective function to maximise the profit.

2)The maximum budget is R10 000 000.

3) Nor barrels R nor barrels E may comprise more than 90% of the total produced barrels.

4) For barrel E ingredient A must be between 40% and 50%, but taking into consideration that ingredient B may not be more than 46%.

5) If more than 20 000 barrels of E are sold the market starts to get saturated. There is a logarithmic decrease in the price, but for practicality you decided to model it linearly. Every barrel above 20 000 of E can only be sold for R135 and every barrel above 30 000 of E can only be sold for R130. Rewrite the objective function with additional constraints (if relevant).

6) A clerk was at error, a barrel of Oil II is not the standard 200 liter barrel, but 130 liter. Rewrite the objective function by taking this information into account.

Oil Ingredient A% Ingredient B% Cost/barrel 35 55 30.00 II 60 25 34.80