1. Formulate algebraically the Linear Programming (LP) model for this problem. Define the decision variables, objective function, and constraints. (18 points)

2. Formulate this same linear programming problem on a spreadsheet and SOLVE using

Excel Solver (Provide the corresponding Excel Spreadsheet and the Answer Report). Include managerial statements that communicate the results of the analyses (i.e.

describe verbally the results). (16 points)

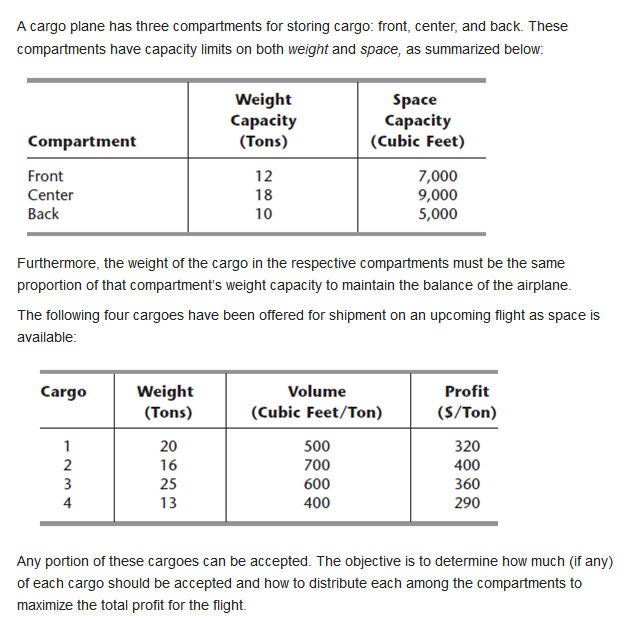
A cargo plane has three compartments for storing cargo: front, center, and back. These compartments have capacity limits on both weight and space, as summarized below: Weight Capacity (Tons) Space Capacity (Cubic Feet) Compartment 12 Front Center Back 18 10 7,000 9,000 5,000 Furthermore, the weight of the cargo in the respective compartments must be the same proportion of that compartment's weight capacity to maintain the balance of the airplane. The following four cargoes have been offered for shipment on an upcoming flight as space is available: Cargo Weight (Tons) Volume (Cubic Feet/Ton) Profit (s/Ton) 20 500 16 1 2 3 4 700 AWN 320 400 360 290 25 13 600 400 Any portion of these cargoes can be accepted. The objective is to determine how much (if any) of each cargo should be accepted and how to distribute each among the compartments to maximize the total profit for the flight. A cargo plane has three compartments for storing cargo: front, center, and back. These compartments have capacity limits on both weight and space, as summarized below: Weight Capacity (Tons) Space Capacity (Cubic Feet) Compartment 12 Front Center Back 18 10 7,000 9,000 5,000 Furthermore, the weight of the cargo in the respective compartments must be the same proportion of that compartment's weight capacity to maintain the balance of the airplane. The following four cargoes have been offered for shipment on an upcoming flight as space is available: Cargo Weight (Tons) Volume (Cubic Feet/Ton) Profit (s/Ton) 20 500 16 1 2 3 4 700 AWN 320 400 360 290 25 13 600 400 Any portion of these cargoes can be accepted. The objective is to determine how much (if any) of each cargo should be accepted and how to distribute each among the compartments to maximize the total profit for the flight