Question: Four functions are given below. Either the function is defined explicitly, or the entire graph of the function is shown. For each, decide whether it
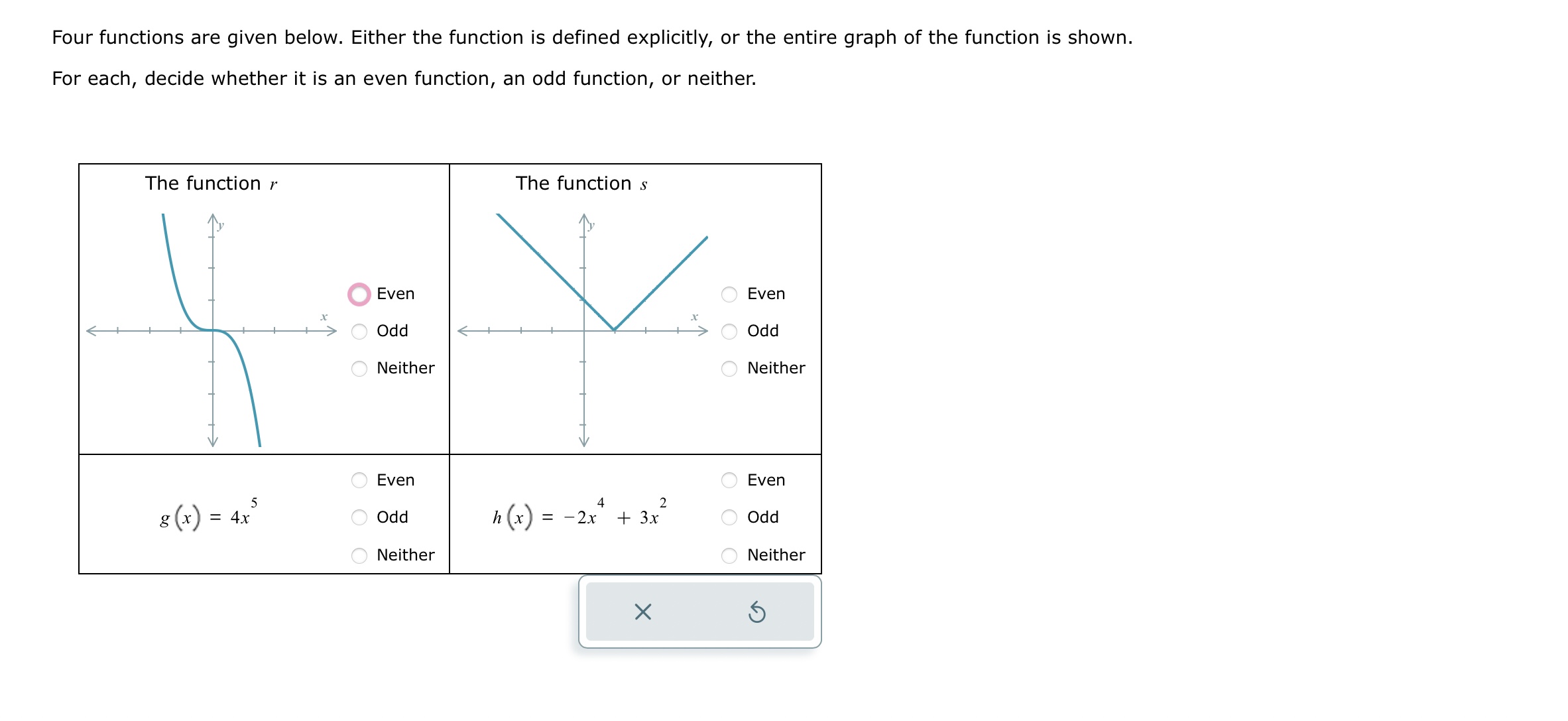
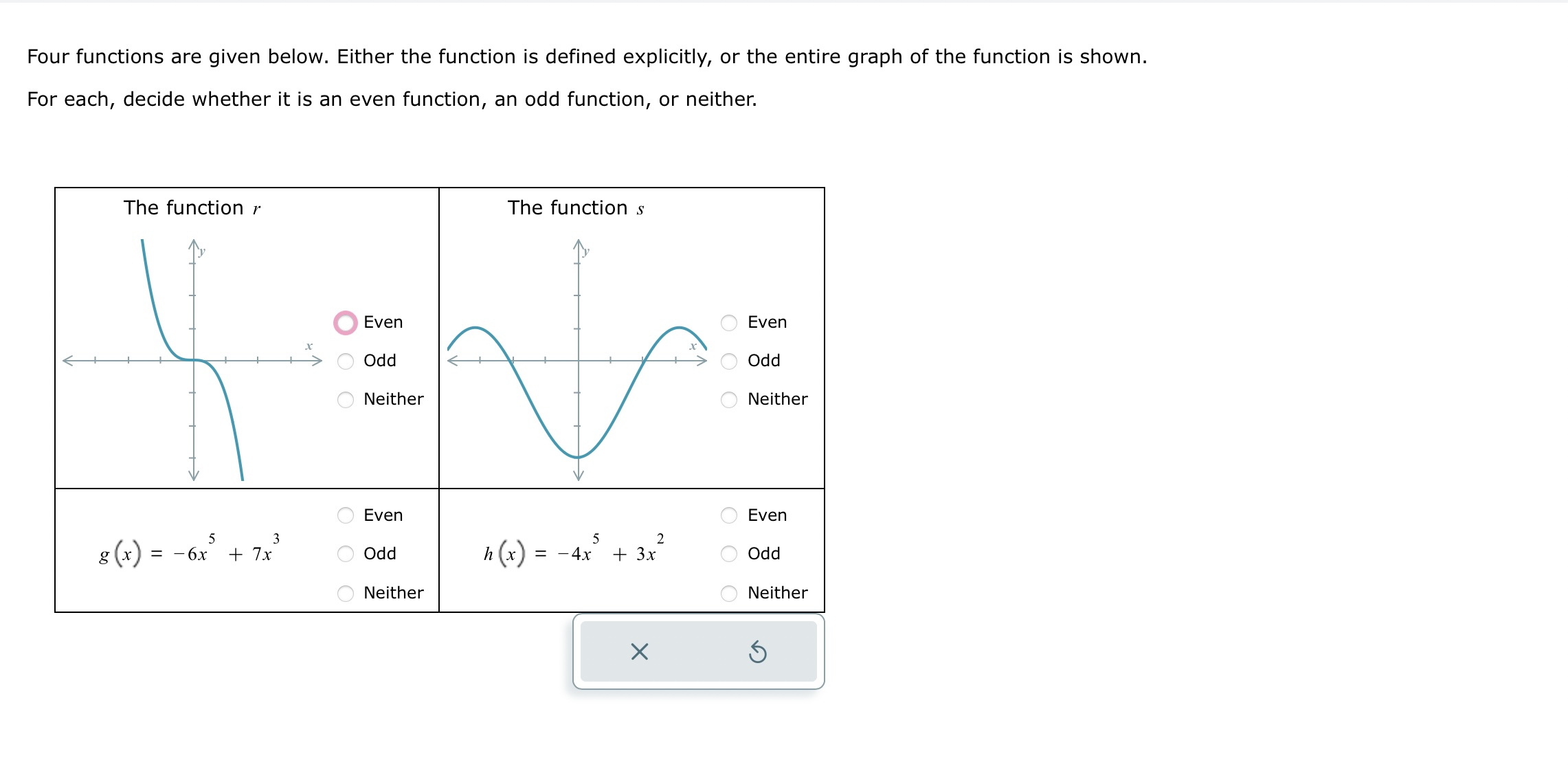
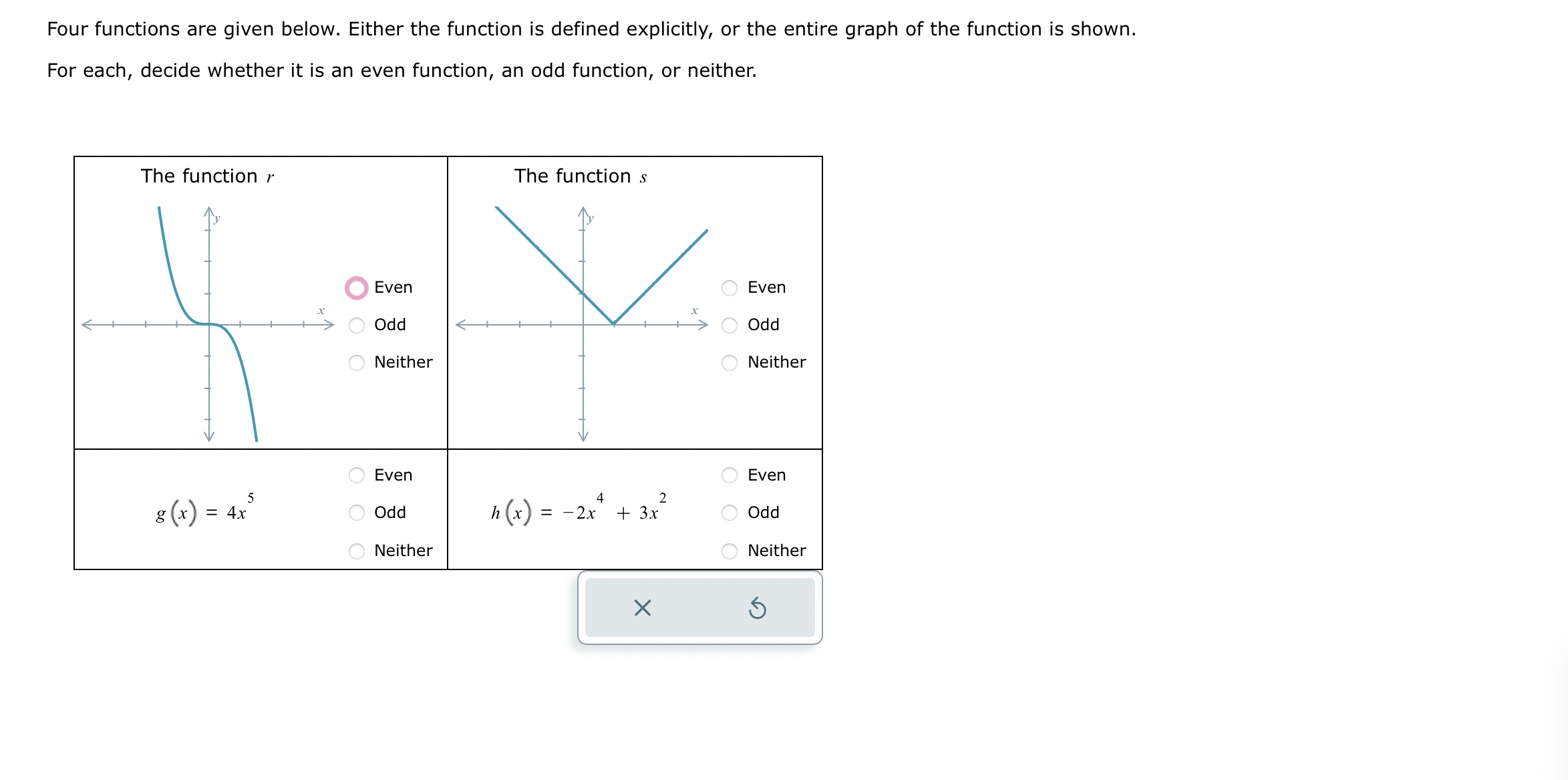
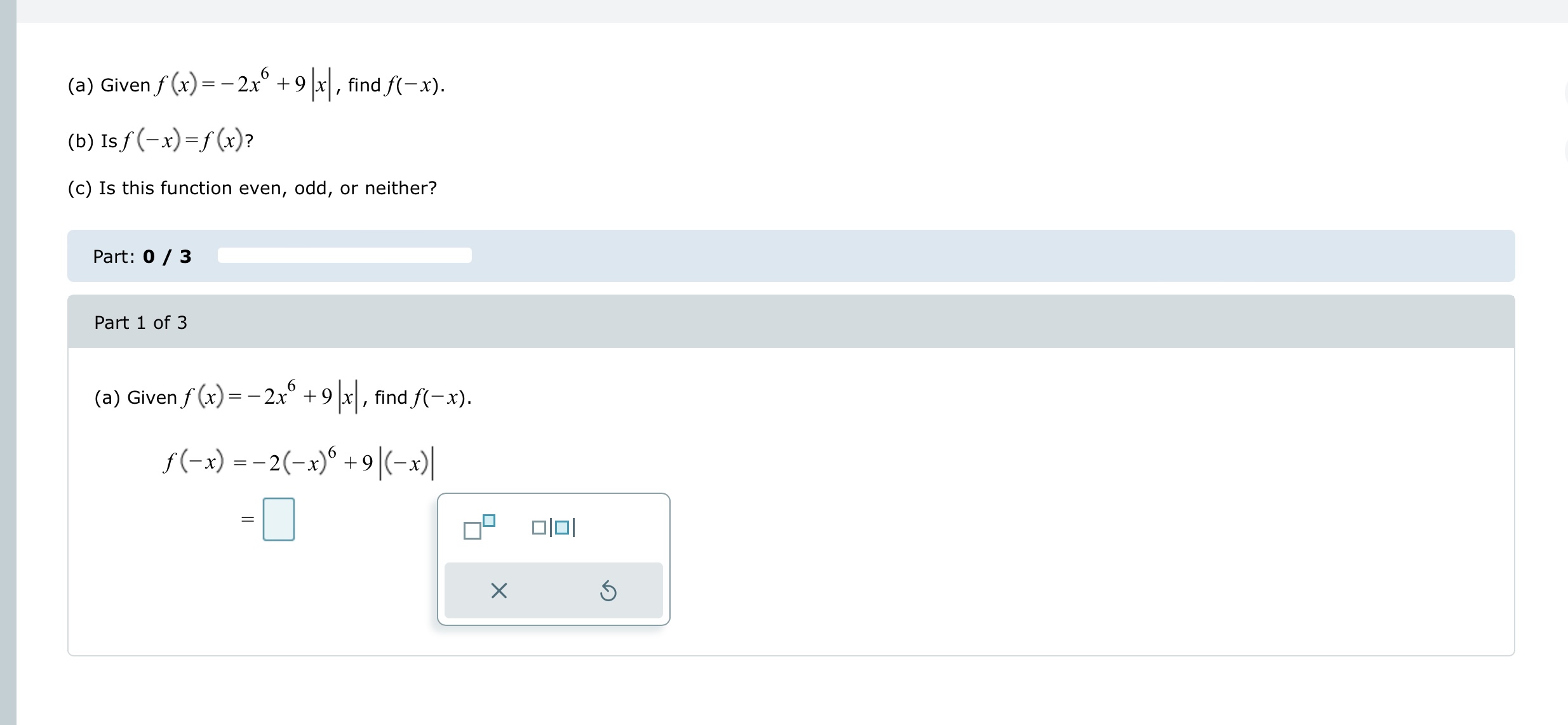
Step by Step Solution
There are 3 Steps involved in it
1 Expert Approved Answer
Step: 1 Unlock


Question Has Been Solved by an Expert!
Get step-by-step solutions from verified subject matter experts
Step: 2 Unlock
Step: 3 Unlock


