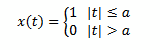
\fProblem 6 Verify Parseval's theorem numerically by using the expression for the Fourier transform of the rectangular pulse you obtained in Problem 2, and the Matlab function: integral (fun, xmin, xmax) which performs a numerical integration of a given function fun from xmin to xmax. Assume a = 1/2. You may use your best judgement to determine suitable values of xmin to xmax . Note: In Matlab, you can define a function fun of a variable x using: fun = @ (x) _expression in terms of x For example, f(x) = e*cos(x") can be defined as fun = @ (x) exp (-x) . *cos (x. *2)