from pulp import LpMinimize, LpProblem, LpStatus, lpSum, LpVariable, LpInteger, GLPK import numpy as np import random randomFloatList = [] Age = 20 #Maximum age f bus (index = i) Time_Period = 100 #Time periods considered (index = j) age = list(range(Age)) time = list(range(Time_Period)) # Create the model model = LpProblem(name="CampusTransportSystem", sense=LpMinimize) # Initialize the decision variables x = {(i,j): LpVariable(name=f"x{i,j}", lowBound=0, cat="Integer") for i in age for j in time} y = {(i,j): LpVariable(name=f"y{i,j}", lowBound=0, cat="Integer") for i in age for j in time} #3... define variables #All should be random values #purchase cost of a bus (v) v = list(np.random.randint(low = 737000, high = 958000, size = 100)) print(list(v)) #number of bus to be purchased p = list(np.random.randint(low = 1, high = 3, size = 100)) print(list(p)) #fuel price per gallon g = list(np.random.randint(low = 2.64, high = 4.46, size = 100)) print(list(g)) #maintenance cost m = list(np.random.randint(low = 7628, high = 8000, size = 100)) print(list(m)) #emission cost e = list(np.random.randint(low = 3040, high = 10145, size = 100)) print(list(e)) #salvage value s = list(np.random.randint(low = 1000, high = 5000, size = 100)) print(list(s)) #utilization cost u = list(np.random.randint(low = 33000, high = 33045, size = 100)) print(list(u)) #fuel economy of a bus for i in range(0, 19): f = round(random.uniform(3.32, 3.65), 20) randomFloatList.append(f) print(randomFloatList) #discount rate #Each term in the model should have a diferent discount rate for i in range(0, 5): r = round(random.uniform(0.0955, 0.1), 5) randomFloatList.append(r) print(randomFloatList) model += lpSum(v[j]*p[j]*(1+r)**(-j) for j in time) + \ lpSum(((g[j]*u[i])/f[i])*x[(i,j)]*(1+r)**(-j) for j in time for i in age) + \ lpSum((m[i]*u[i])*x[(i,j)]*(1+r)**(-j) for j in time for i in age) + \ lpSum(u[i]*e*x[(i,j)]*(1+r)**(-j) for i in age for j in time) - \ lpSum(s[i]*y[(i,j)]*(1+r)**(-j) for j in time for i in age) type(expression) # Add the constraints to the model for j in time: model += v[j]*p[j] = d[j] for i in age: for j in time: model += [x[(i-1,j-1)]] == [x[(i,j)] + y[(i,j)]] for j in time: model += [x[(M,j)]] == 0 for j in time: model += [y[(0,j)] ] == 0 type(constraint) # Solve the problem status = model.solve() print(f"status: {model.status}, {LpStatus[model.status]}") print(f"objective: {model.objective.value()}") for var in model.variables(): print(f"{var.name}: {var.value()}") for name, constraint in model.constraints.items(): print(f"{name}: {constraint.value()}") model.variables() model.variables()[0] is x model.variables()[1] is y

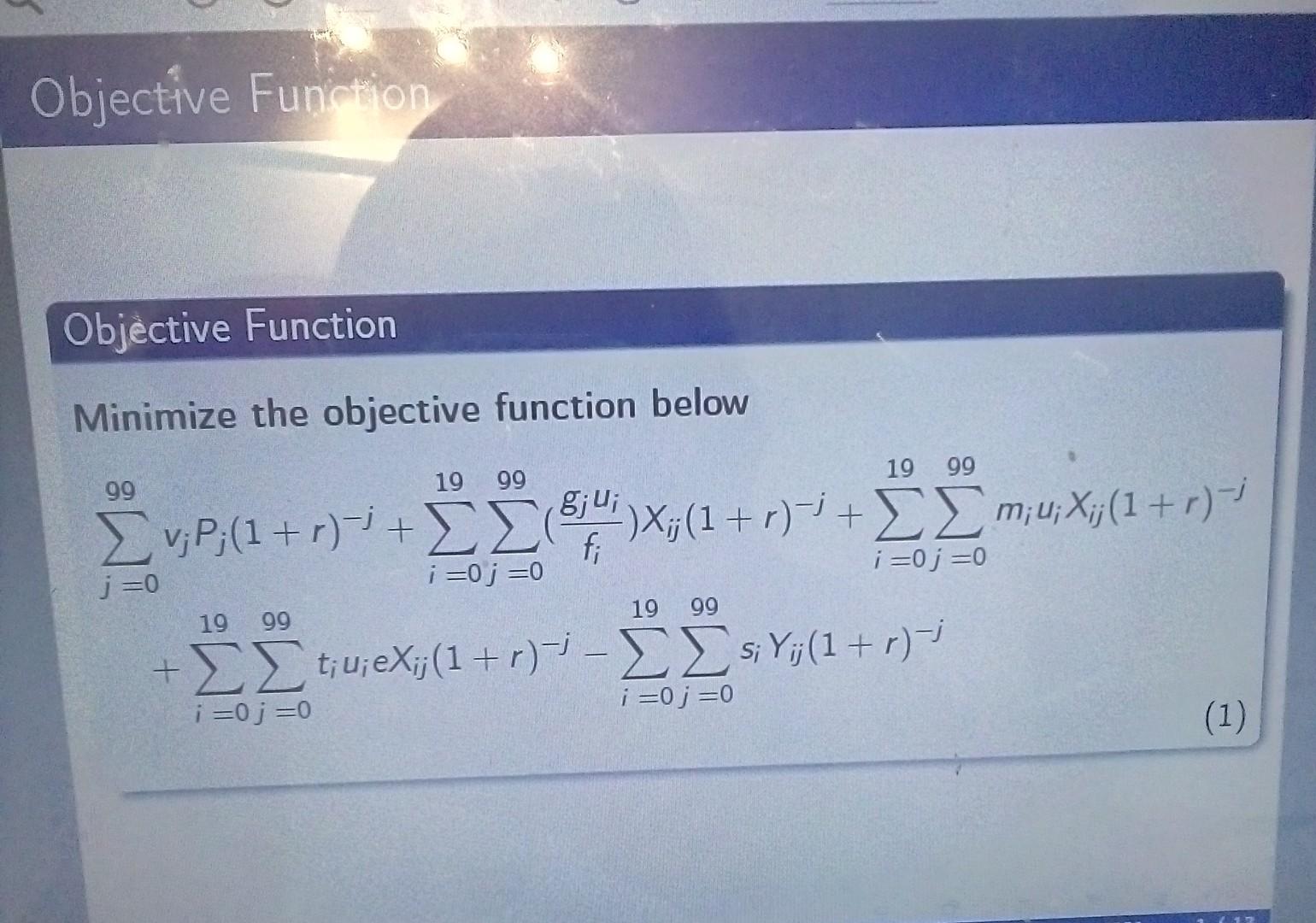
Objective Function Objective Function Minimize the objective function below 99 1999 99 19 v;P;(1+r)-i + )x;(1+r)-i + m; v;X;(1+r) - i=0; =0 j=0 i=j=0 19 99 19 99 + t;u;eXij(1+r) - si Yj(1+r)- i=j=0 i=0;=0 (1)