Question: From various textbooks, I have read that: (1) When a sequence s n as n x one writes that the x lim s n =
From various textbooks, I have read that:
(1) When a sequencesnasnxone writes that thexlimsn=if forM>0,Nsuch that if n > N thensn> M.
(2) When a sequencesnasnxone writes that thenlimsn=xlimsn=if forM0,Nsuch that if n > N thensn I think I canusethese two definitionstohelpme prove thefollowingtheorem given that the proof requires metoconsideracasewherethelimitmirrors (1)andthe othercasemirrors (2). However, these definitions might be unnecessary. whatarethe proofsforthe two casesinthefollowingtheorem.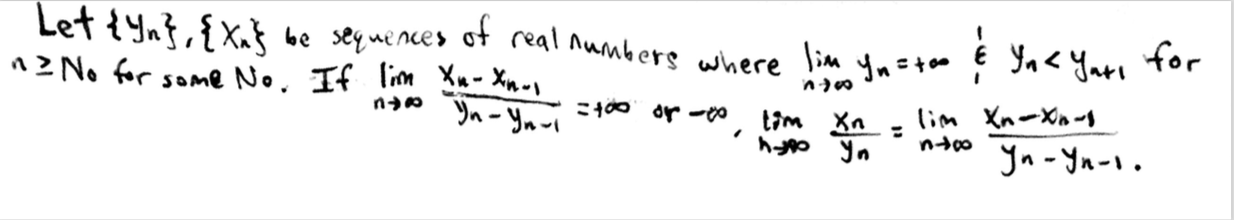
Step by Step Solution
There are 3 Steps involved in it

Get step-by-step solutions from verified subject matter experts


