Question: fStandard Normal Distribution Table (page 2) Area - Standard Normal Distribution 0.00 1.01 0.02 0.03 1.04 0.05 0.06 0.07 1.08 0.09 0.0 0.5000 0.5040 0.5080

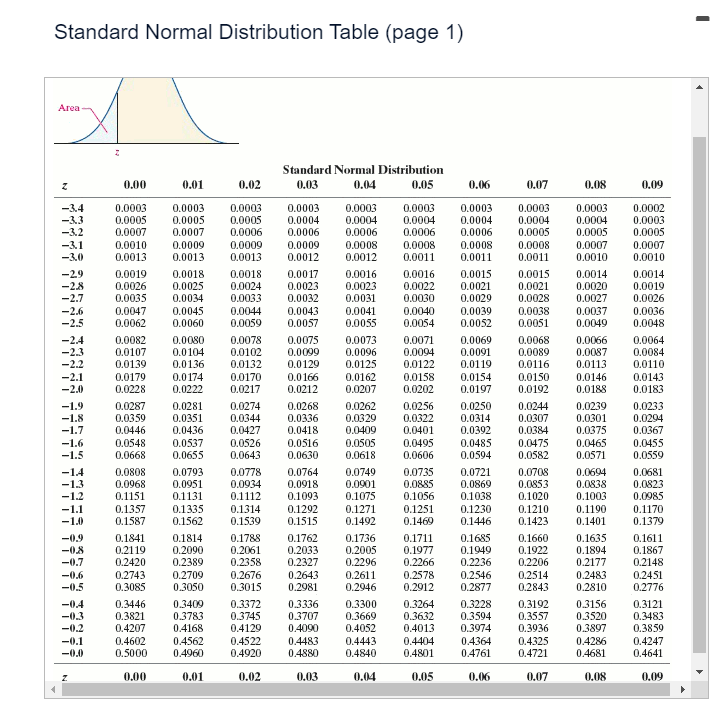
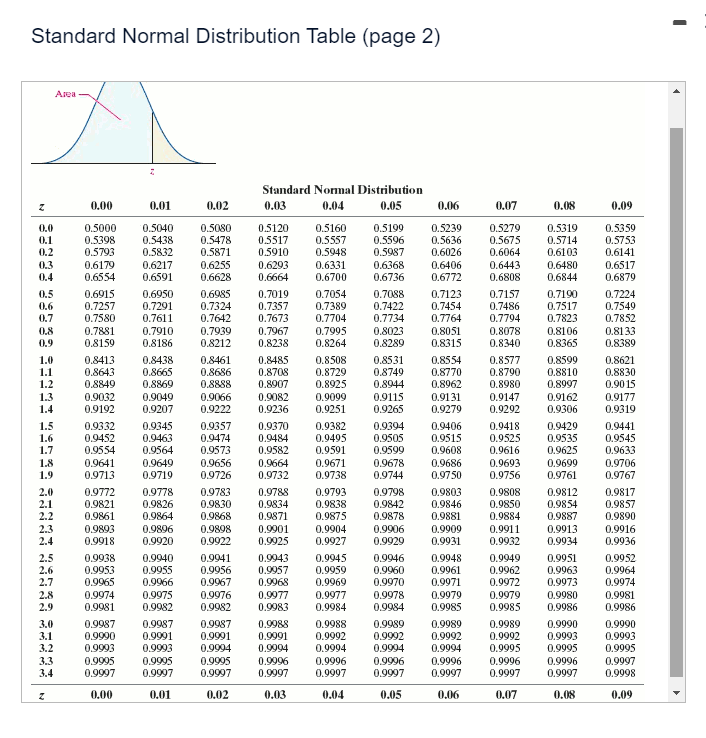
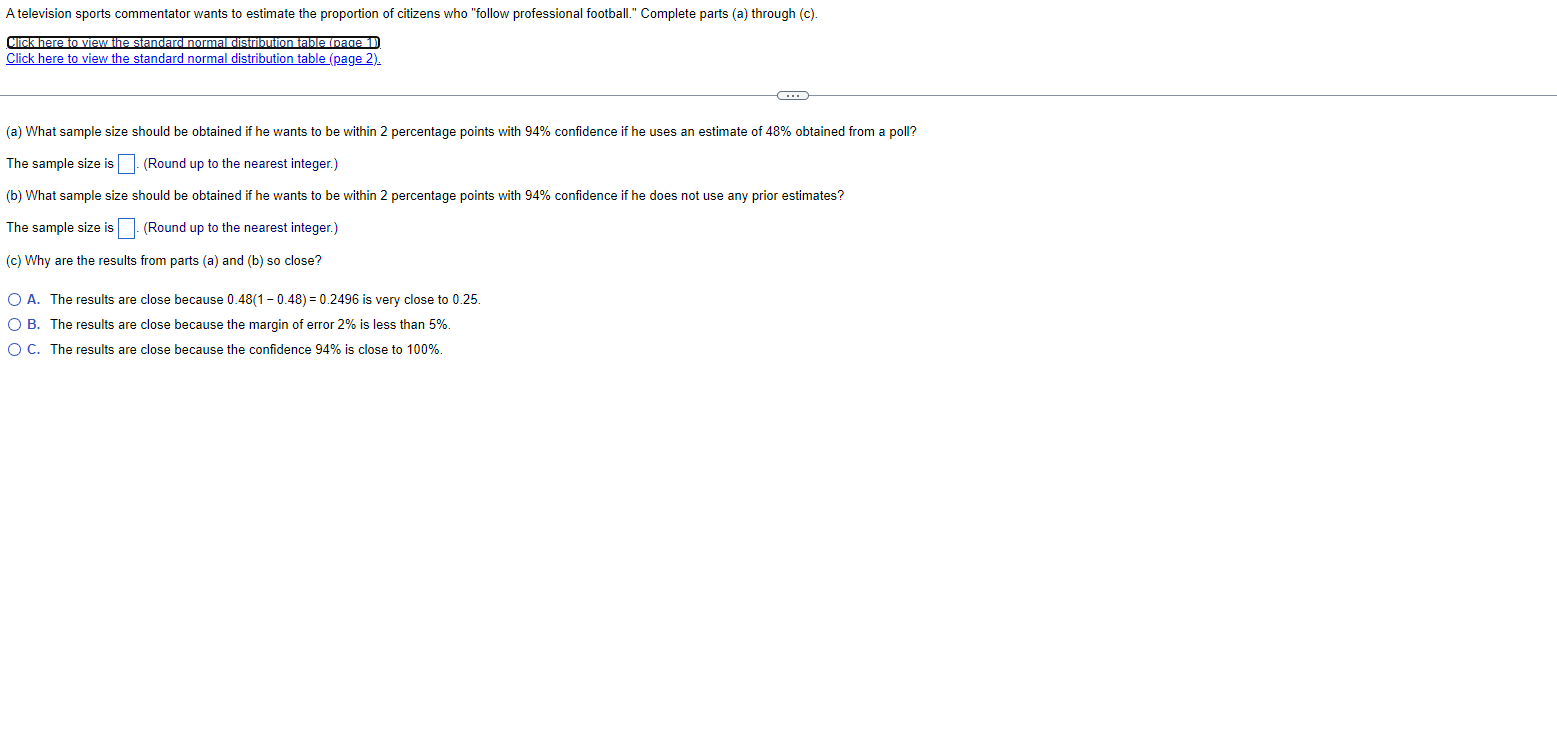
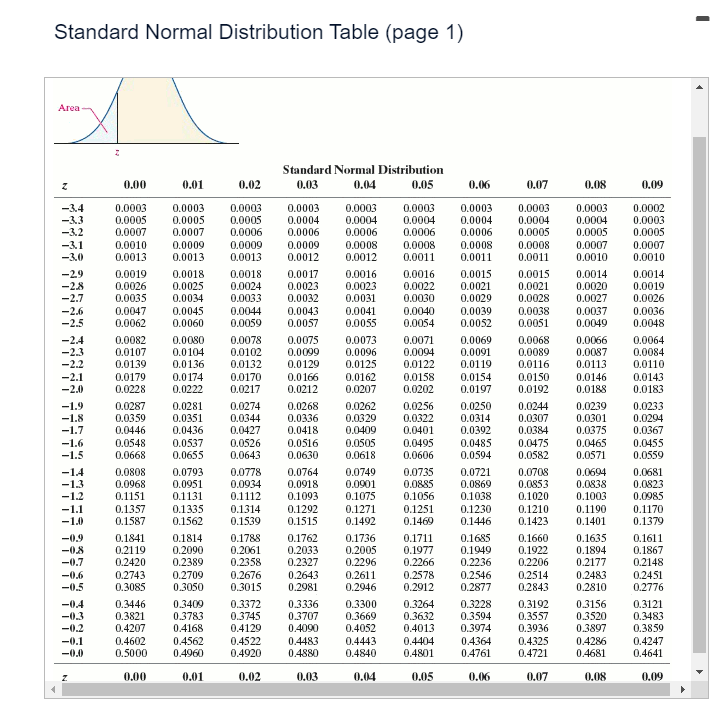
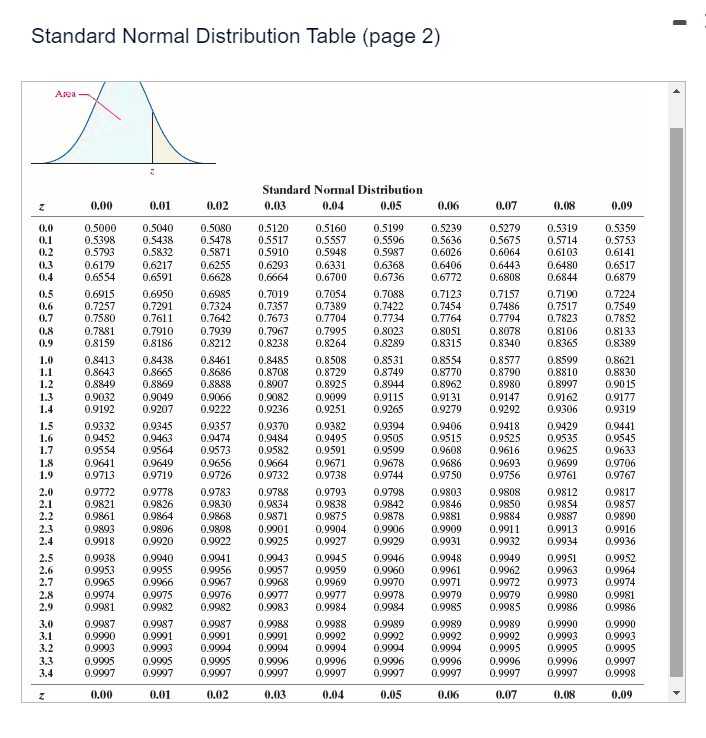
$\fStandard Normal Distribution Table (page 2) Area - Standard Normal Distribution$ 0.00 1.01 0.02 0.03 1.04 0.05 0.06 0.07 1.08 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 3.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438

0.5478 0.5517 0.5557 0.5596 0.5636 D.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871

0.5910 0.5948 0.5987 0.6026 0.6064 0.61 03 0.6141 0.3 0.6179 0.6217 0.6255

\fStandard Normal Distribution Table (page 2) Area - Standard Normal Distribution 0.00 1.01 0.02 0.03 1.04 0.05 0.06 0.07 1.08 0.09 0.0 0.5000 0.5040 0.5080 0.5120 0.5160 0.5199 3.5239 0.5279 0.5319 0.5359 0.1 0.5398 0.5438 0.5478 0.5517 0.5557 0.5596 0.5636 D.5675 0.5714 0.5753 0.2 0.5793 0.5832 0.5871 0.5910 0.5948 0.5987 0.6026 0.6064 0.61 03 0.6141 0.3 0.6179 0.6217 0.6255 0.6293 0.6331 0.6368 0.6406 0.6443 0.6480 0.6517 0.4 0.6554 0.6591 0.6628 0.6664 0.6700 0.6736 0.6772 D.6808 0.6844 0.6879 0.5 0.6915 0.6950 0.6985 0.7019 0.7054 0.7058 0.7123 0.7157 0.7190 0.7224 0.6 0.7257 0.7291 0.7324 0.7357 0.7389 0.7422 0.7454 0.7486 0.7517 0.7549 0.7 0.7580 0.7611 0.7642 0.7673 0.7704 0.7734 0.7764 0.7794 0.7823 0.7852 0.8 0.7881 0.7910 0.7939 0.7967 0.7995 0.8023 0.8051 0.8078 0.8106 0.8133 0.9 0.8159 0.8186 0.8212 0.8238 0.8264 0.8289 0.8315 D.8340 0.8365 0.8389 1.0 0.8413 0.8438 0.8461 0.8485 D.8508 0.8531 0.8554 0.8577 0.8599 0.8621 1.1 0.8643 1.8665 0.8686 0.8708 0.8729 0.8749 0.8770 0.8790 1.8810 0.8830 0.8997 1.2 0.8849 0.8869 0.8888 0.8907 0.8925 0.8944 0.8962 0.8980 0.90 15 1.3 0.9032 0.9049 0.9056 0.9082 1.9099 0.9115 0.9131 0.9147 0.91 62 0.9177 1.4 0.9192 0.9207 0.9222 0.9236 D.9251 0.9265 0.9279 D.9292 0.9306 0.9319 1.5 0.93.32 0.9345 0.9357 0.9370 D.9382 0.9394 0.9406 0.9418 0.9429 0.9441 1.6 0.9452 0.9463 0.9474 0.9484 0.9495 0.9505 0.9515 0.9525 0.9535 0.9545 1.7 0.9554 0.9564 0.9573 0.9582 0.9591 0.9599 0.9608 0.9616 0.9625 0.9633 1.8 0.9641 0.9649 0.9656 0.9664 0.9671 0.9678 0.9686 0.9693 0.9699 0.9706 1.9 0.9713 0.9719 0.9726 0.9732 0.9738 1.9744 0.9750 0.9756 0.9761 0.9767 2.0 0.9772 0.9778 0.9783 0.9788 0.9793 0.9798 0.9803 0.9808 0.9812 0.9817 2.1 0.9821 0.9826 0.9830 0.9834 1.9838 1.9842 1.9846 1.9850 1.9854 0.9857 2.2 0.9861 0.9864 0.9868 0.987 0.9875 0.9878 0.9881 0.9884 0.9887 0.9890 2.3 0.9893 1.9896 1.9898 0.9901 0.9904 1.9906 0.9909 0.9911 0.9913 0.9916 2.4 0.9918 0.9920 1.9922 0.9925 1.9927 0.9929 1.9931 0.9932 .9934 0.9936 2.5 0.9938 0.9040 0.9041 0.9943 0.9945 0.9046 0.9948 0.9049 0.9951 0.9952 2.6 0.9964 0.9953 0.9955 0.9956 0.9957 0.9959 0.9960 0.9961 0.9962 0.9963 2.7 0.9965 0.9966 0.9967 0.9968 0.9969 0.9970 0.9971 0.9972 0.9973 0.9974 2.8 0.9974 0.9975 1.9976 0.9977 0.9977 0.9978 0.9979 0.9979 3.9980 0.9981 2.9 0.9981 1.9982 1.9982 0.9983 0.9984 0.9954 0.9985 0.9985 0.9986 0.9986 0.9987 0.9987 0.9087 0.9088 0.9988 1.9989 3.9989 0.9989 0.9090 0.9990 3.0 3.1 0.9990 0.9991 0.9991 0.9991 0.9992 0.9992 0.9992 0.9992 0.9993 0.9993 3.2 0.9993 0.9993 0.9994 0.9994 1.9994 0.9994 0.9994 D.9995 0.9995 0.9995 3.3 0.9995 0.9995 0.9095 0.9096 0.9996 0.9096 0.9096 0.9996 0.9096 0.9997 0.9997 0.9997 1.9997 0.9997 0.9997 0.9997 0.9997 D.9997 0.9997 0.9998 0.00 0.01 0.02 1.03 0.04 0.05 0.06 0.07 0.08 0.09A television sports commentator wants to estimate the proportion of citizens who "follow professional football." Complete parts (a) through (c). Click here to view the standard normal distribution table (page 1) Click here to view the standard normal distribution table (page 2). (a) What sample size should be obtained if he wants to be within 2 percentage points with 94% confidence if he uses an estimate of 48% obtained from a poll? The sample size is ]. (Round up to the nearest integer.) (b) What sample size should be obtained if he wants to be within 2 percentage points with 94% confidence if he does not use any prior estimates? The sample size is | |. (Round up to the nearest integer.) (c) Why are the results from parts (a) and (b) so close? O A. The results are close because 0.48(1 - 0.48) = 0.2496 is very close to 0.25. O B. The results are close because the margin of error 2% is less than 5%. O C. The results are close because the confidence 94% is close to 100%

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

You are the operations manager of a firm that uses the continuous inventory control system. Suppose the firm operates 50 weeks a year, 350 days, and has the following characteristics for its primary...

3) (25 points) Suppose that the price of a share of stock follows the Black-Scholes model dS(t) = 0.20S(t)dt +0.40S(t)dz(t) where t donotes the time in years. The current price is S(0) = 100 and the...

1. Sam's Cat Hotel operates 52 weeks per year, 7 days per week and uses a continuous review inventory system. It purchases kitty litter for $11.50 per bag. The following information is available...

Please help me. Please show all work so I am able to understand how to do the problem. Choose the best answer for the following statements. 11. Rejecting the null hypothesis when it is true is called...

6) A high-school senior is concerned about attending college because she knows that many college students require more than 4 years to complete a bachelor's degree. The student goes to a college...

1) On the Minnesota's department of fish and game website there was an article that stated the mean age of Coyotes in the northern region is 1.75 years. A biologist specializing in wildlife in the...

5) A survey in Men's Health magazine reported that 39% of cardiologists said that they took vitamin E supplements. A random sample of 1500 cardiologists found that 36% of them took vitamin E...

Determine the sample size n needed to construct a 90% confidence interval to estimate the population proportion for the following sample proportions when the margin of error equals 4%. a. p=0.30 b....

The diameters of ball bearings are distributed normally. The mean diameter is [25 millimeters and the variance is 25. Find the probability that the diameter of a selected bearing is greater than 130...

J-Rata Corp shares are currently trading at $30 each. It is expected to increase by 10% or decrease by 6% during the next two-three months. If its strike price at maturity in six months is set as $32...

Multiple-Choice Questions 1. A business owner makes 1,000 items a day. Each day he or she contributes eight hours to produce those items. If hired, elsewhere he or she could have earned $250 an hour....

Farleigh Petroleum, Inc., is a small company that acquires high-grade crude oil from low-volume production wells owned by individuals and small partnerships. The crude oil is processed in a single...

31. Obtain all data that is necessary from the worksheet prepared for Healthy Eating Foods Company in Problem 12.5A at the end of Chapter 12. Then follow the instructions to complete this problem....

true or false when telephone services internet connections and skilled employees are expensive or not readily available for the country such are called infrastructure challenges

7. Also complete the following sentence: This core value is important to me when I ________________________. This is the situation this core value is important to you we are looking for here.

9. What type of competence is important to have and develop in order to strengthen the core value you want others to associate with you?

6. Identify a core value that is important to you and that you would like to strengthen in yourself. Write down this core value. Then complete the follow-ing sentence: This core value is important to...