Full explanation needed

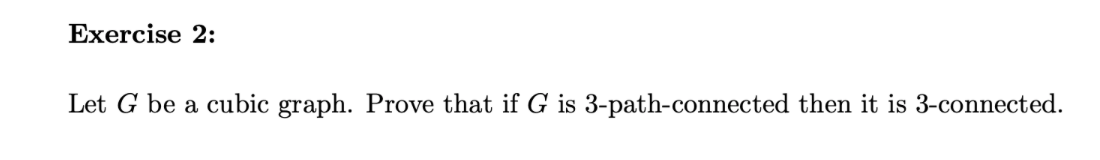
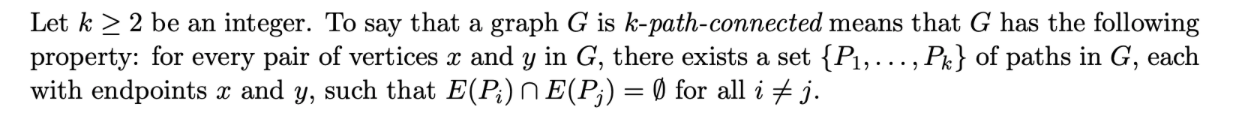
Exercise 2: Let G be a cubic graph. Prove that if G is 3-path-connected then it is 3-connected.Let k 2 2 be an integer. To say that a graph G is k-path-connected means that G has the following property: for every pair of vertices x and y in G, there exists a set { P1, ..., PK} of paths in G, each with endpoints x and y, such that E(Pi) n E(P;) = 0 for all i # j