Full question is below, but the image is broken up, so I have typed out:

Consider the entrance region of a cylindrical tube of radius R, as shown in figure 4.19. The inlet velocity profile is uniform, with the velocity Uo. The fluid is Newtonian in the flow study. Within the entrance region, the velocity field Vz is two-dimensional. Downstream, the velocity field is fully developed in depends on Y (please use correct symbol) only. Use the integral forms of the conservation of linear momentum and mass for steady flow to relate the drag force exerted by the fluid on the walls of the tube to the pressure drop in the entrance region.

THANK YOU SO MUCH FOR YOUR HELP!!!

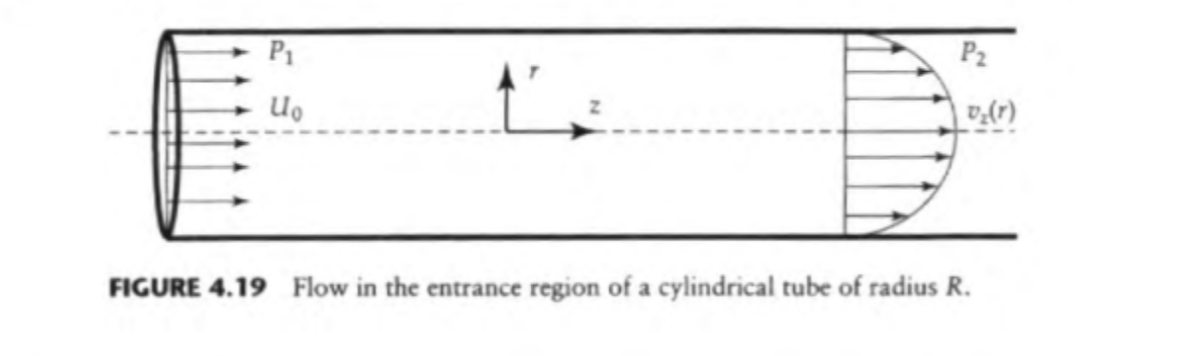
4.3 Consider the entrance region of a cylindrical tube of radius R, as shown in Figure 4.19. The inlet velocity profile is uniform, with velocity U0. The fluid is Newtonian and the flow is steady. Within the entrance region, the velocity field vz is two dimensional. Downstream, the velocity field is fully developed and depends on r only. Use the integral forms of the conservation of linear momentum and mass for steady flow to relate the drag force exerted by the fluid on the walls of the tube to the pressure drop in the entrance region. FIGURE 4.19 Flow in the entrance region of a cylindrical tube of radius R. Problem 3. Textbook problem 4.3. (15 pts.) Additional notes to better explain this problem and to provide hints for how to solve it: 1. Assume that the flow channel is horizontal, and thus there is no influence from gravity. 2. For this problem, there is uniform velocity at the entrance of the tube (i.e., v2=U0= constant; not a function of r), which then stabilizes to a fully developed parabolic flow profile downstream away from the entrance where vz=f(r). Thus, because the velocity profiles at the inlet and outlet of the volume to be analyzed are different, the surface integral representing the sum of the entrance and exit velocity terms of the integrated linear momentum balance (i.e., v(vn^)dS ) is not equal to zero. 3. When you calculate the values for Sv(vn^)dS (i.e., one expression for the entrance where the velocity profile is uniform and then one expression for where the downstream flow is fully developed and a function of ' r '), represent the velocity in the integral for the downstream flow as a function of r and the average velocity over the cross-sectional area, v (i.e., v2=f(v2,r). We derived an expression that can be used for this relationship previously in class for the condition of fully developed flow, so check your lecture notes. For the entrance, vz=U0= constant =v2 (i.e., not a function of r )