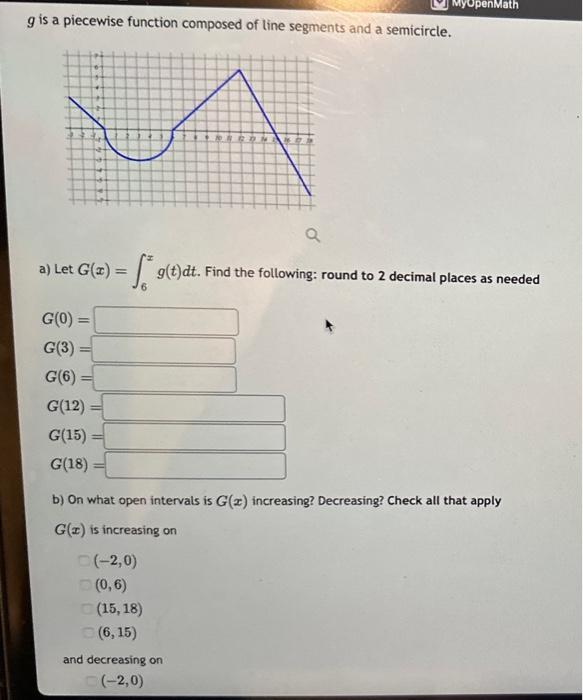
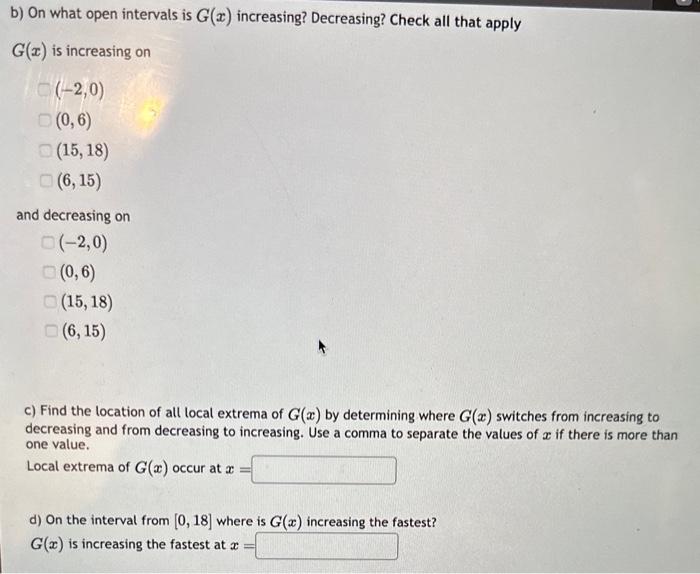
g is a piecewise function composed of line segments and a semicircle. a) Let G(x)=6xg(t)dt. Find the following: round to 2 decimal places as needed G(0)=G(3)=G(6)=G(12)=G(15)=G(18)= b) On what open intervals is G(x) increasing? Decreasing? Check all that apply G(x) is increasing on (2,0)(0,6)(15,18)(6,15) and decreasing on b) On what open intervals is G(x) increasing? Decreasing? Check all that apply G(x) is increasing on (2,0)(0,6)(15,18)(6,15) and decreasing on (2,0)(0,6)(15,18)(6,15) c) Find the location of all local extrema of G(x) by determining where G(x) switches from increasing to decreasing and from decreasing to increasing. Use a comma to separate the values of x if there is more than one value. Local extrema of G(x) occur at x= d) On the interval from [0,18] where is G(x) increasing the fastest? G(x) is increasing the fastest at x=