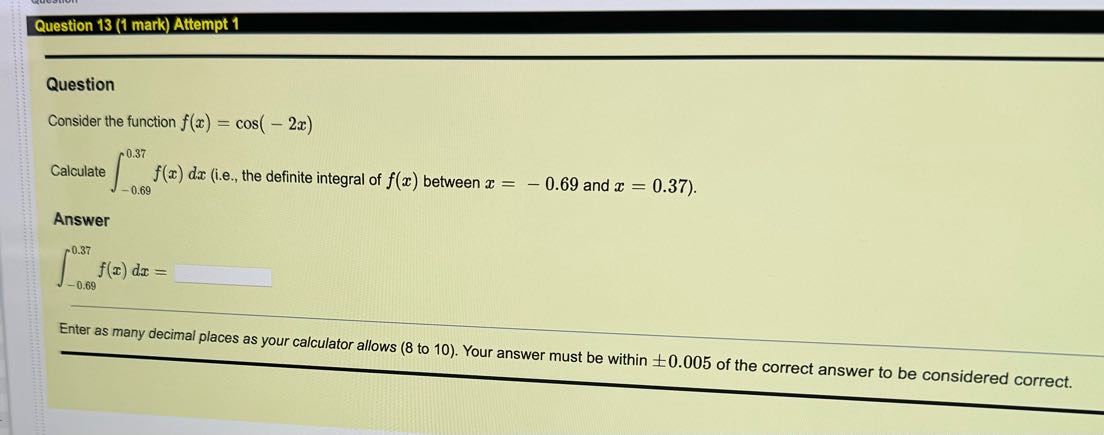
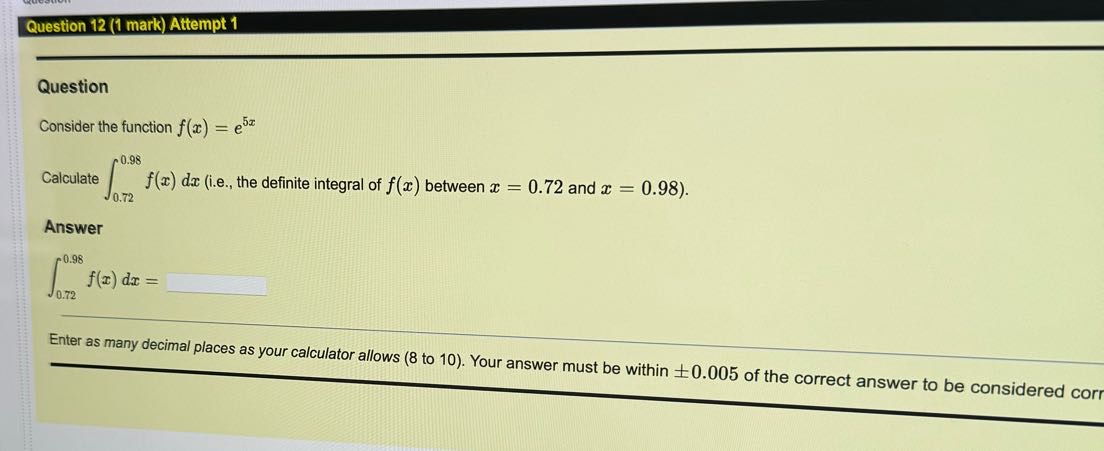
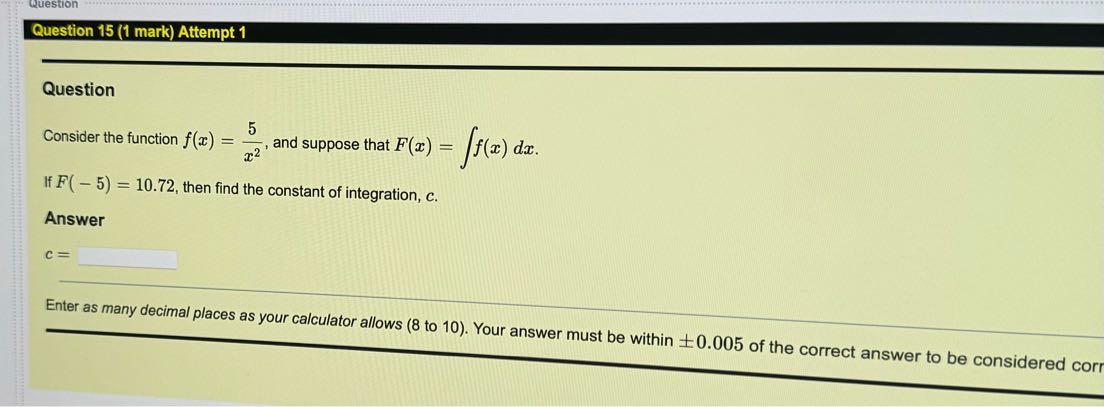
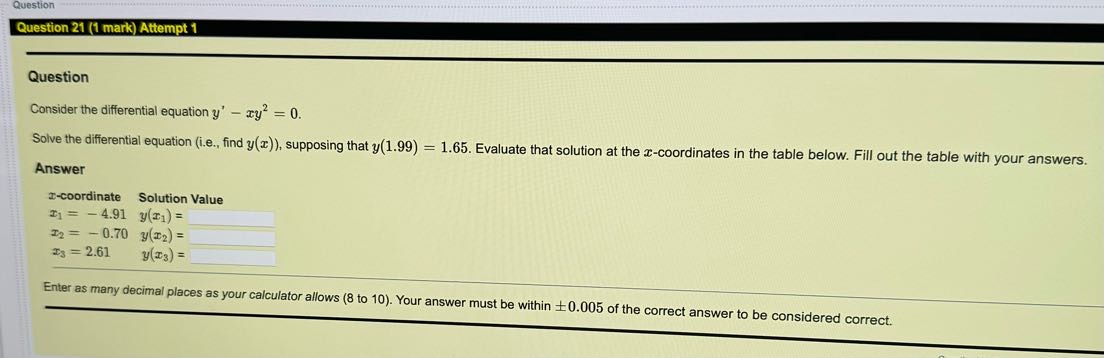
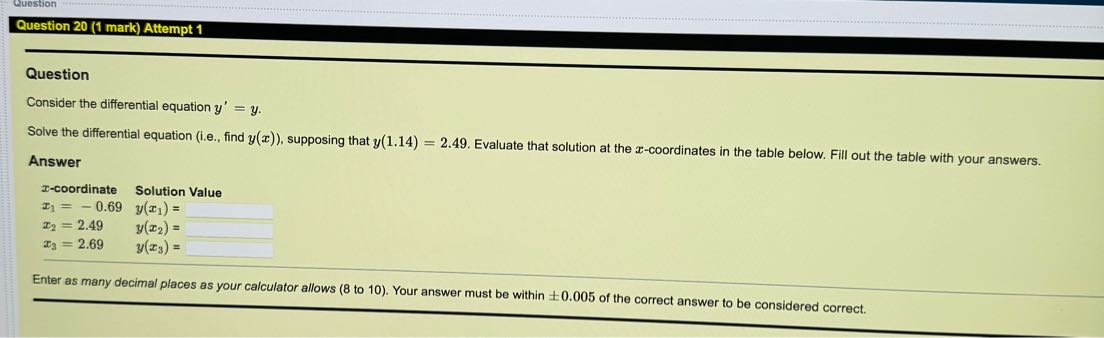
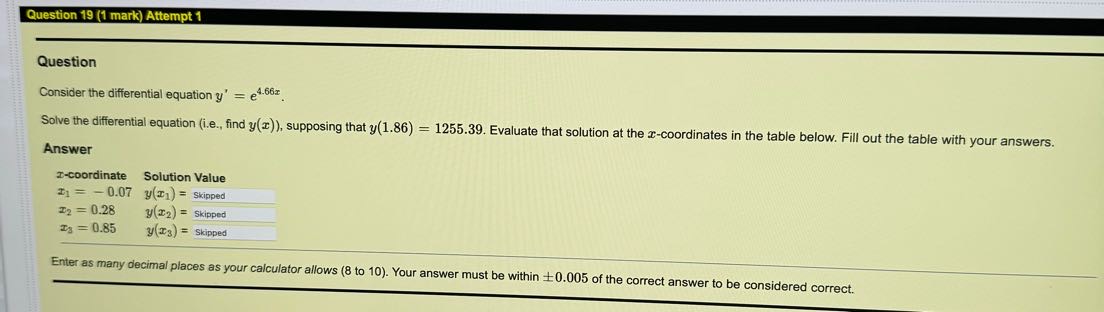
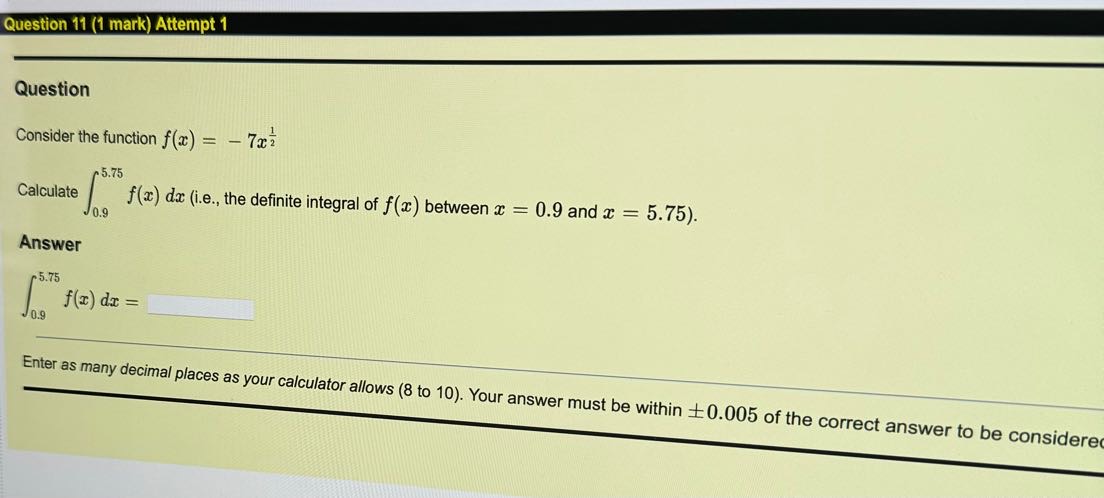
g Question 13 (1 mark) Attempt 1 _m-spa __ 0, Question Consider the function f(z) = cos( 2z) 037 Calculate f - 0.69 f(2) dz (i, the definite integral of f(z) between z = 0.69 and z = 0.37). Question 18 (1 mark) Attempt 1 Question Consider the function f(x) = cos( - 3x), and suppose that F(x) = f(x) dx. If F( - 9) = - 6.19, then find the constant of integration, c. Answer C= Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct anQuestion 12 (1 mark) Attempt 1 Question Consider the function f (a) = e5z .0.98 Calculate f(x) da (i.e., the definite integral of f(x) between x = 0.72 and x = 0.98). Jo.72 Answer 0.98 f(x) dr = 0.72 Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct answer to be considered cornQuestion 16 (1 mark) Attempt 1 Question Consider the function f(x) = 2x7, and suppose that F(x) = f(x) da. If F(2) = - 0.33, then find the constant of integration, c. Answer C = Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct answer to be considered correct.Question Question 15 (1 mark) Attempt 1 _h_________ Question 5 Consider the function f(z) = , and suppose that F'(z) = /:f(:c) dz. &L i F( 5) = 10.72, then find the constant of integration, c. Answer Cc= Enter as many decimal Places as your calculator allows (8 to 10). Your answer must be within - =0.005 of the correct answer to be considered corr Question Question 21 (1 mark) Attempt 1 Question Consider the differential equation y' - xy = 0. Solve the differential equation (i.e., find y(x)), supposing that y(1.99) = 1.65. Evaluate that solution at the I-coordinates in the table below. Fill out the table with your answers. Answer -coordinate Solution Value 1 = - 4.91 y(21) = 12 = - 0.70 y(12) = Is = 2.61 y(T3) = Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within 10.005 of the correct answer to be considered correct.tuestion Question 20 (1 mark) Attempt 1 Question Consider the differential equation y' = y. Solve the differential equation (i.e., find y(r)), supposing that y(1.14) = 2.49. Evaluate that solution at the x-coordinates in the table below. Fill out the table with your answers. Answer r-coordinate Solution Value T1 = - 0.69 y(=) = T2 = 2.49 y(X2) = T3 = 2.69 y(x3) = Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within 10.005 of the correct answer to be considered correct.e e R T e | Question Consider the 1% order linear differential equation y' + 'y = g(w) for some function g(z). Use the integrating factor method to find the integrating factor for this differential equation (recall that I(z) = e /7 (=)42) Evaluate that integrating factor at the z-coordinates in the table below. Fill out the table with your answers, Answer r-coordinate Integrating Factor Ty = 050 I(z,)= 3= (.08 I(z;) = 3 = (.BR f{:a}: Enter as many decimal Places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct answer to be considered correct Question 17 (1 mark) Attempt 1 Question Consider the function f(z) = %%, and suppose that F(z) = /f(m} dz. if F( 2) = 7.58, then find the constant of integration, e. Answer Enter as many decimal places as your calculator allows e (8 to 10). Your answer must be within = 0.005 of the correct answer to be considered correct. Question 14 (1 mark) Attempt 1 Question Consider the function f(x) = - 4x*, and suppose that F(x) = f(x) dx. If F( - 5) = 2494.79, then find the constant of integration, c. Answer C = Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct answer to be considered correctQuestion Question 23 (1 mark) Attempt 1 Question Consider the differential equation y' + cos(x)y = cos(x). Solve the differential equation (i.e., find y(x)), supposing that y( - 8.69) = 2.07. Evaluate that solution at the r-coordinates in the table below. Fill out the table with your answers. Answer a-coordinate Solution Value I1 = -8.80 y(=1) = 12 = - 2.20 y(12) = Is = 4.60 Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within +0.005 of the correct answer to be considered correct.Question 19 (1 mark) Attempt 1 Question Consider the differential equation y' = e4-66r Solve the differential equation (i.e., find y(r)), supposing that y(1.86) = 1255.39. Evaluate that solution at the r-coordinates in the table below. Fill out the table with your answers. Answer -coordinate Solution Value $1 - -0.07 y(1 ) = Skipped 12 = 0.28 y(12) = Skipped Is = 0.85 y(13) = Skipped Enter as many decimal places as your calculator allows (8 to 10). Your answer must be within + 0.005 of the correct answer to be considered correct.Question 11 (1 mark) Attempt 1 h Question Consider the function f(z) = 722 " = = 5.75). Calculate f() dz (i.e., the definite integral of f(x) between z = (0.9 and z ) Answer 5.75 f(z) dz = 0. Enter as man Y decimal places as Your calculator allows (810 10) - Your answer must be within +0.005 of the correct answer to pe considereg