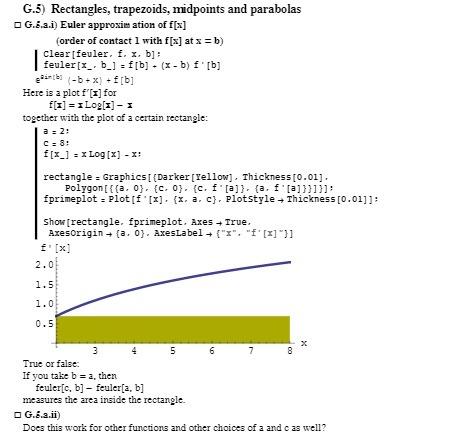
Question: G.5) Rectangles, trapezoids, midpoints and parabolas O G.6.a.i) Euler approxim ation of f[x] (order of contact ] with f[x] at x = b) Clear [feuler,

G.5) Rectangles, trapezoids, midpoints and parabolas O G.6.a.i) Euler approxim ation of f[x] (order of contact ] with f[x] at x = b) Clear [feuler, f. x. b] : feuler [x_ . b_] = f[b] - (x - b) f '[b] gaincel ( -b + x] + f[b] Here is a plot f'[x] for f [x] = x Log[x] - I together with the plot of a certain rectangle: a = 2: C = 8: f [x_ ] = x Log [x] - X: rectangle = Graphics [{Darker [Yellow] . Thickness [0.01] . Polygon [{ {a. 0] . (c. 0]. (c. f' [a]], (a. f'[a]])])]: fprimeplot = Plot[f ' [x], (x. a. c]. PlotStyle + Thickness [0.01]]: Show [rectangle. fprimeplot. Axes + True. AxesOrigin 4 {a, 0}. AxesLabel + {"x". "f' ")] f' [x] 2.0 1.5 1.0 0.5 3 4 5 6 7 True or false. If you take b = a, then feuler[c. b] - feuler[a, b] measures the area inside the rectangle. 0 G.6.a.ii) Does this work for other functions and other choices of a and c as well

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock blur-text-image

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

.............. (1 point) (a) Estimate the area under the graph of f (x) = 4 + x2 from x = 1 to x = 2 using three approximating rectangles and right endpoints. R3=[17 ] (b) Repeat part (a) using six...

The purpose of this project is to combine many of the skills learned in class into one graphical user interface. This interface should be easy to read, organized, and free from errors. Teams of two...

Estimate the area under the graph of f (x) over the interval [3, 8] using ten approximative rectangles and right endpoints as sample points. Rn Repeat the approximation using left endpoints as sample...

Estimate the area under the graph of f(I) 6 over the interval [0, 13] using 10 approximationg rectangles and midpoints as sample points. M10 Repeat the approximation using using 50 approximationg...

Estimate the area under the graph of f(x) = x + 4 over the interval [0, 15] using 10 approximating rectangles and midpoints as sample points. M10 = Repeat the approximation using using 50...

1. Find the function f(x) if f"(x) = x/ - 2x + 4, f(1) = 2 and f(0) = -1. 2. In class, we guessed using approximations that the area under f(x) = x on the interval [0, 1] is approximately 0.25. Use...

Question 1 2 pts A definite integral is the limit of a Riemann sum of an infinite number of infinitesimally thin O None of these O Triangles O Rectangles Trapezoids

Approximate the values of definite integrals using rectangles, trapezoids, and parabolas. Estimate the value of dx by using n =4 subintervals of equal width using the X + 1 trapezoidal rule. Round...

Please provide steps and explanations if possible. 1) Express the following limit as a definite integral: lim Et ~sin (-1 + 3i n O- 2 cos( x) dx Of3 sin (x) dx OfA sin ( -2 + x) dx 2 cos ( x) dx O 2...

Through a calculation (on Canadian Individual Tax Returns) known as the Old Age Security claw back, an individual receiving Old Age Security (OAS) benefits must repay an increasing portion of these...

12)What mass of H2SO4 is contained in 25g of 15% w/w solution? (Relative atomic mass are H=1amu , S=32amu, O=16amu)

Regardless of other factors, ownership of less than 2 0 % of another company's voting shares must always be considered a passive investment. True false question. True False

Compare leadership and followership in a paragraph or two. form a table with two columns comparing leadership and followership with at least five characteristics for each. Explain the formal and...