Gaussian function solutions

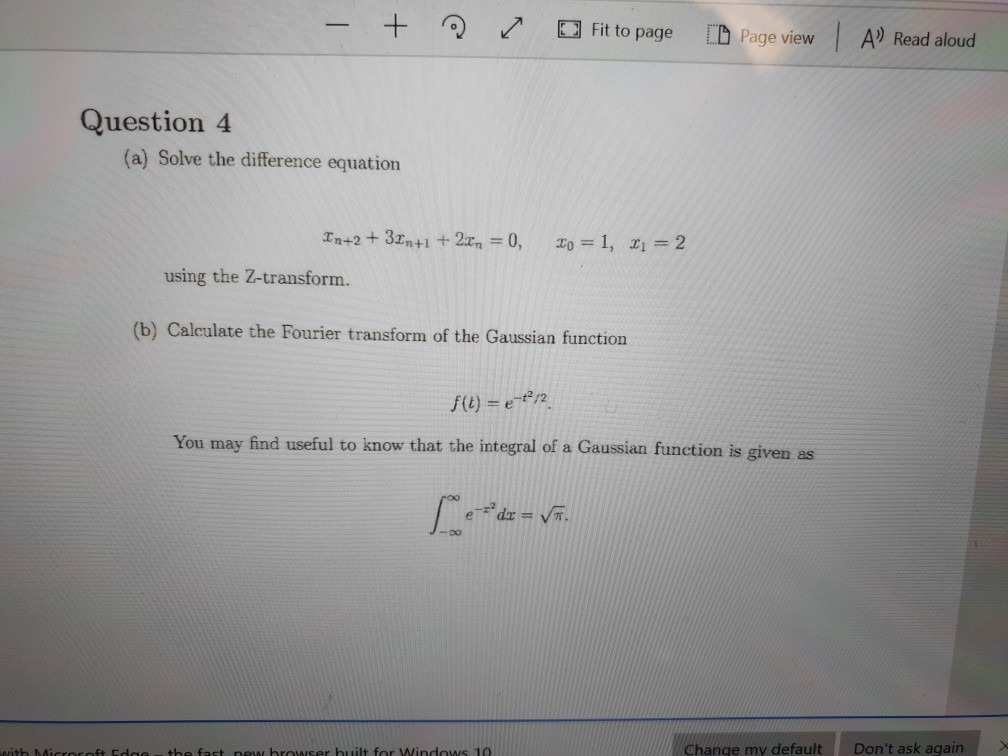
6. The (normalized) Gaussian function is defined as 1 -12 g(r) = OV2x where (_g(x)dr = 1. Note that this implies that the "DC component" of its Fourier transform G(0) = 1. Prove that the Fourier transform is also a Gaussian function of the form -w202 G(w) = e Hint: Use the differentiation with respect to t, and multiplication properties of the Fourier transform, and then integrate both sides.+ 2 Fit to page [ Page view A') Read aloud Question 4 (a) Solve the difference equation In+2 + 3En+1 + 21 = 0, 10 = 1, $1 = 2 using the Z-transform. (b) Calculate the Fourier transform of the Gaussian function f (t) = e- +212 You may find useful to know that the integral of a Gaussian function is given as Change my default Don't ask again2. A Gaussian function f(x) is given by the formula f(I) = Ae 107, where A is a constant, and the constant o, gives a measure of the spread or width of the shape. Find the Fourier transform f(k) of f(x) and show that the it is also a Gaussian function of the form f (k) = Be 3x Find the width ox and show that the produet a,ox - 1