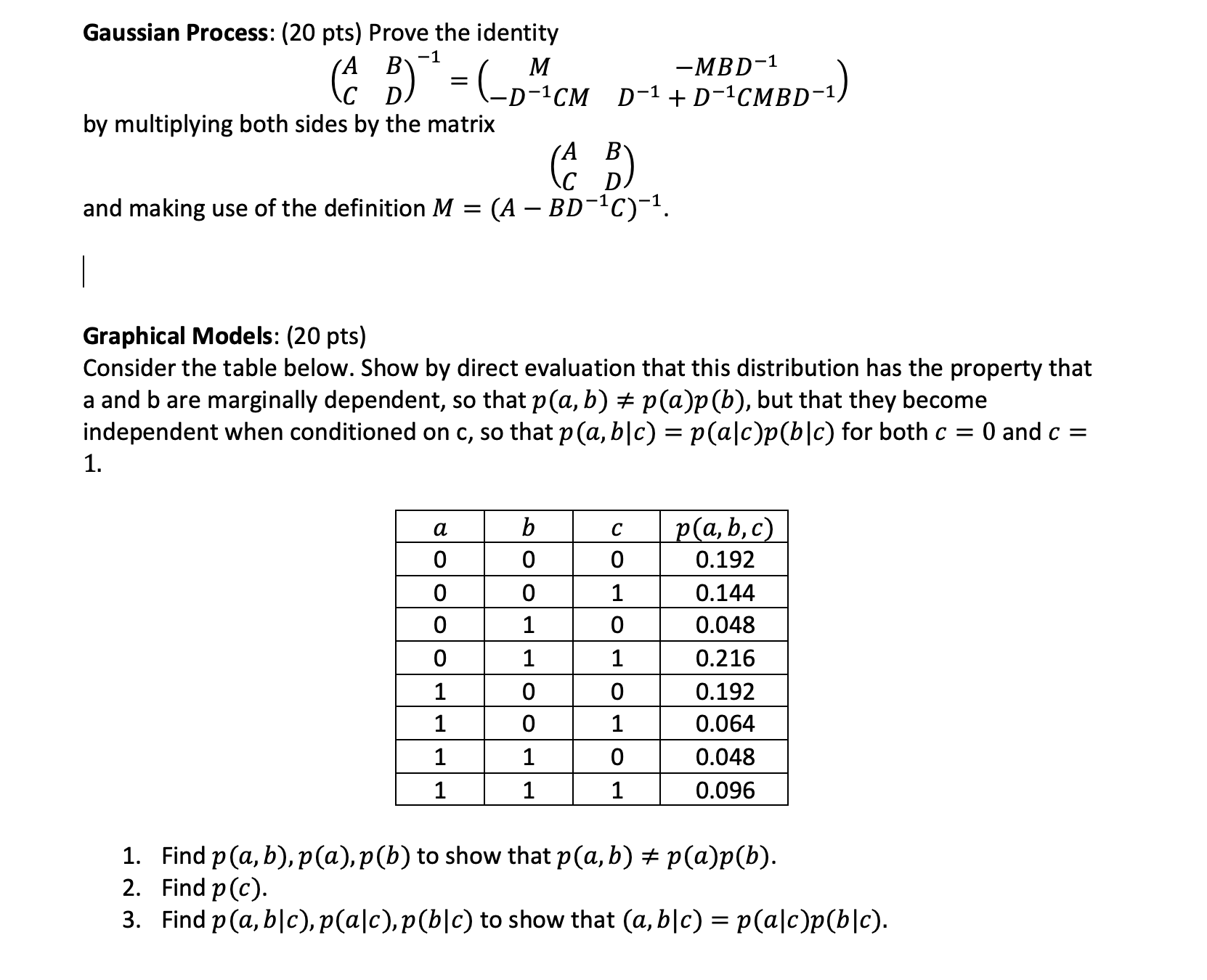
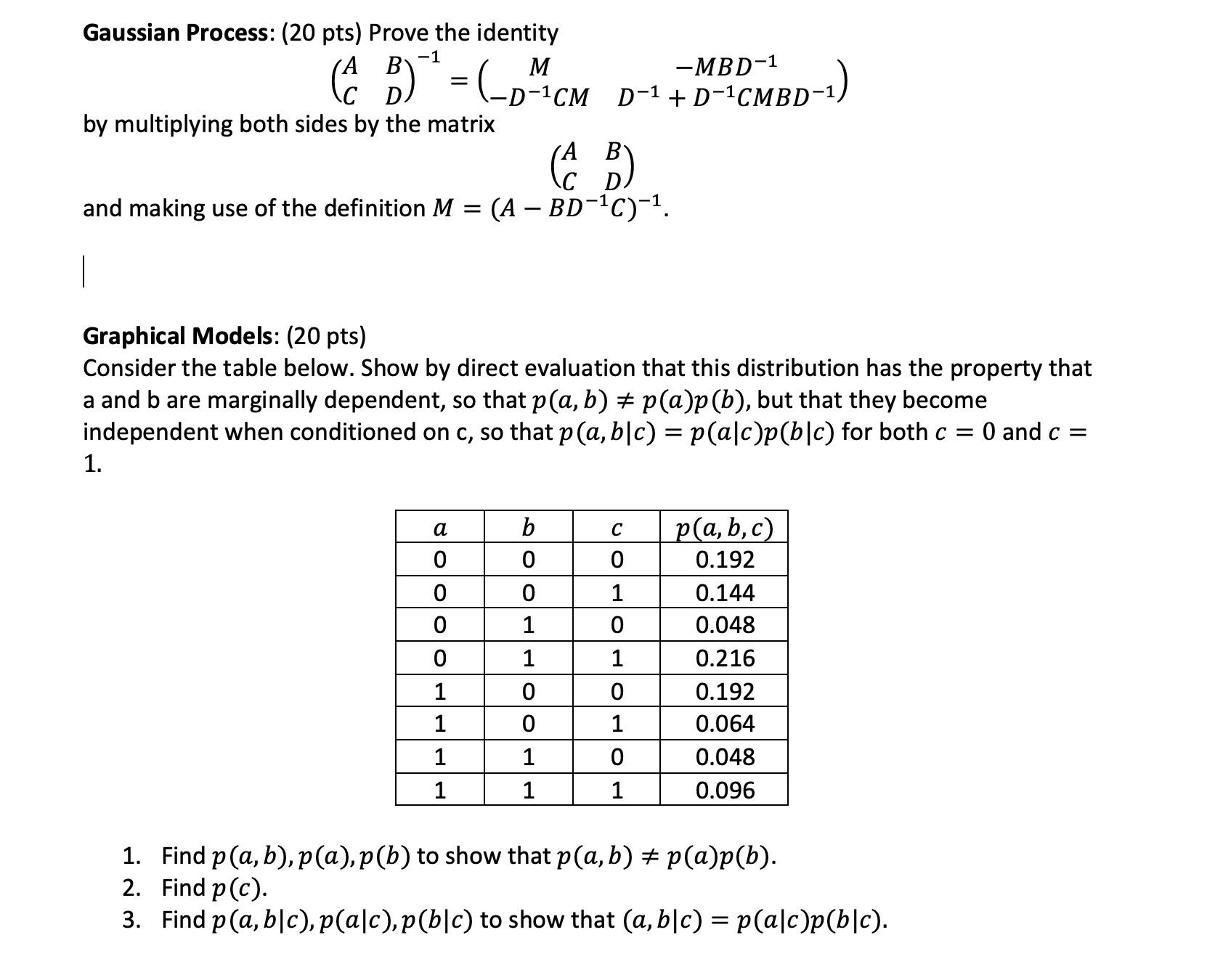
Gaussian Process: (20 pts) Prove the identity -MBD-1 ( C D ) = ( - D-ICM D-1 + D-1CMBD -1) by multiplying both sides by the matrix (A D and making use of the definition M = (A - BD-1C) -1. Graphical Models: (20 pts) Consider the table below. Show by direct evaluation that this distribution has the property that a and b are marginally dependent, so that p(a, b) + p(a)p(b), but that they become independent when conditioned on c, so that p (a, b|c) = p(alc)p(b|c) for both c = 0 and c = 1. C p(a, b, c) 0 0 0 0.192 0 0.144 0 0 0.048 0 0.216 0 0.192 1 0 0.064 0 0.048 1 1 0.096 1. Find p (a, b), p(a), p(b) to show that p(a, b) # p(a)p(b). 2. Find p (c). 3. Find p(a, b|c), p(alc), p(b|c) to show that (a, b|c) = p(alc)p(b|c)